How do you solve the inequality #(x-1)(x+4)(x-3)>0#?
1 Answer
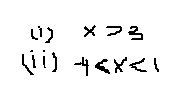
Explanation:
There can be three situations for the inequality to hold good:
I.All terms are positive that means
II
III
IV
Analyzing the above options, it would be clear that II is not possible, because x cannot be greater than 1 and less than -4 at the same time.
Like wise IV is also not possible because x can not be greater than -3 and less than -4 at the same time
Hence I and III are the only solutions for the Inequality.
