How do you solve the right triangle ABC given b=3, B=26?

Question

4994 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-14T17:10:27

See below.

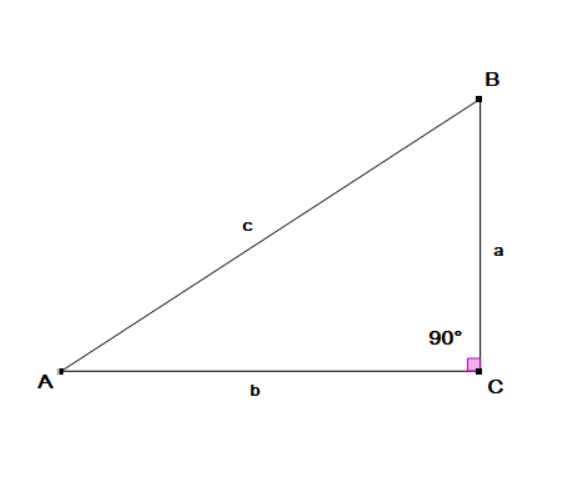
enter image source here

I am assuming #B= 26# refers to the measurement of angle B in degrees.

Listing what we know already:

Angle A = #90^o-26^o= 64^o#

Angle B = #26^o#

Angle C = #90^o#

Side b = 3

Since we know all three angles and one side, we can use the Sine Rule to solve this:

#sinA/a=sinB/b=sinC/c#

We will use #sinA/a=sinB/b# , because we know angles A and B and we know b.

So:

#sin(64)/a=sin(26)/3=> a= (3sin(64))/sin(26)= 6.151# (3 .d.p)

By Pythagoras' Theorem:

#c^2 = a^2 +b^2#

#c^2= ((3sin(64))/sin(26))^2 + 3^2=> c=sqrt(((3sin(64))/sin(26))^2 + 3^2)= 6.844# ( 3 .d.p)

So we have solved the right angled triangle:

#a = 6.151# (3 .d.p)

#b= 3#

#c= 6.844# ( 3 .d.p)

#A = 64^o#

#B= 26^o#

#C = 90^o#