How do you solve the system by graphing #y= 1/4x -1# and #y= -2x -10#?
2 Answers
Explanation:
the given system
Solution
Transpose all terms with x on the left side
Multiply now both sides by 4/9
to solve for
Checking
With equation
~~~~~~~~~~~~~~~~~~~~~~~
Checking
With equation
God bless....I hope the explanation is useful
Solution by graphing below.
Explanation:
For each of the given equations select a few (at least two but I would suggest three) values for
Plot each pair of points which you have calculated and draw a line for each equation's set of points.
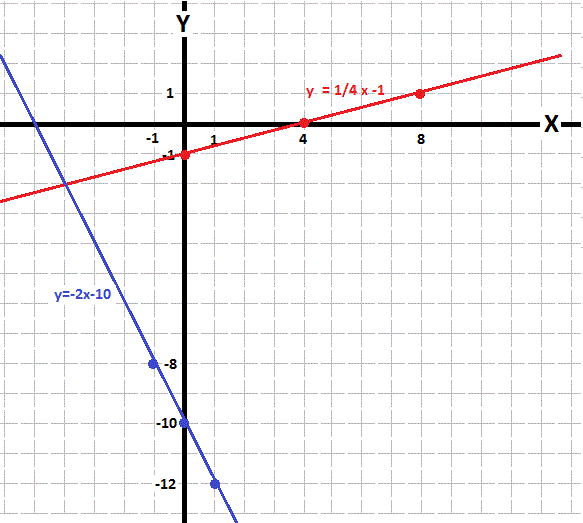
The point where the two equation lines intersect provide the coordinates of the system solution.
In this case it appears that
(This in fact the exact solution but, in general, solving equations by graphing is very dependent on the accuracy of your drawing).
