How do you solve the system by graphing #y = 2x + 1# and #y = 2x - 2#?
1 Answer
Aug 11, 2018
The system of linear equation are inconsistent.
The inconsistent system has no solution.
Explanation:
We have , both the eqn. are in Slop-intercept form:
#ul(|x=|color(white)(,.,)0 | color(white)(.....)1|color(white)(...)-2|#
#ul(|y=|color(white)(,..)1|color(white)(.....)3|color(white)(...)-3|#
#ul(|x=|color(white)(,.,)0 | color(white)(.....)2|color(white)(...)-1|#
#ul(|y=|color(white)(.)-2|color(white)(.....)2|color(white)(...)-4|#
Plot the graph of both equations.
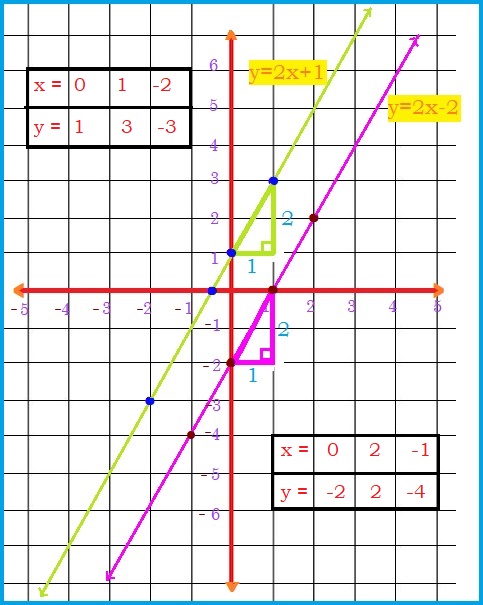
We can see that both the lines are parallel and never intersect each other.
The system of linear equation are inconsistent.
The inconsistent system has no solution.

