How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent $3 x - y = 9$ $3x-y=9$ and $2 x + y = 6$ $2x+y=6$ ?

Question

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent $3 x - y = 9$ $3x-y=9$ and $2 x + y = 6$ $2x+y=6$ ?

1 Answer

Impact of this question

1439 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-08T09:55:58

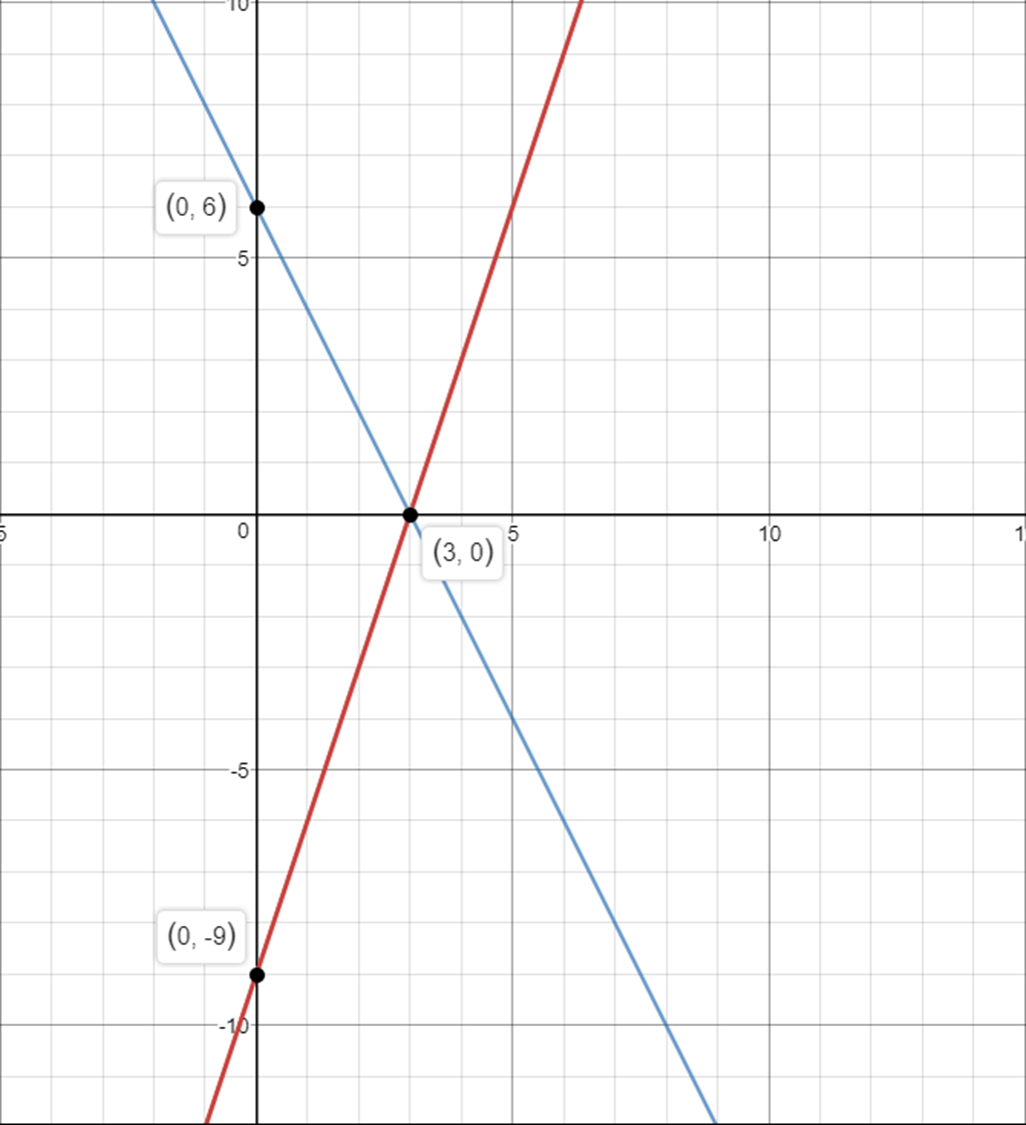
$(3, 0)$ $(3,0)$

Explanation:

Given -

$3 x - y = 9$ $3x-y=9$ -------------(1)
$2 x + y = 6$ $2x+y=6$ -------------(2)

If the slopes are different, both are consistent, else inconsistent.

When the equations are in the form

$a x + b y = c$ $ax+by =c$
The formula for slope is $m = - \frac{a}{b}$ $m=- a/b$
Slope of the first line $m_{1} = - \frac{3}{- 1} = 3$ $m_1=- 3/(-1)=3$
Slope of the second line $m_{2} = - \frac{2}{1} = 2$ $m_2=- 2/1=2$

The slopes are different. They are consistent.

We have to find the intercepts for the two lines to graph them

y-intercept of the 1st line

$3 (0) - y = 9$ $3(0)-y=9$
$y = - 9$ $y=-9$
$(0, - 9)$ $(0, -9)$

x-intercept of the 1st line

$3 x - (0) = 9$ $3x-(0)=9$
$x = \frac{9}{3} = 3$ $x=9/3=3$
$(3, 0)$ $(3,0)$

y-intercept of the 2nd line

$2 (0) + y = 6$ $2(0)+y=6$
$y = 6$ $y=6$
$(0, 6)$ $(0,6)$

x-intercept of the 2nd line

$2 x + 0 = 6$ $2x+0=6$
$x = \frac{6}{2} = 3$ $x=6/2=3$
$(3, 0)$ $(3, 0)$

[ $(3, 0)$ $(3, 0)$ is a common point for both the lines. Hence it is the solution]

enter image source here

Science

Math

Humanities

... and beyond

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent $3 x - y = 9$ $3x-y=9$ and $2 x + y = 6$ $2x+y=6$ ?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent 3x-y=93x−y=93x-y=9 and 2x+y=62x+y=62x+y=6?

1 Answer

Explanation:

Related questions

Impact of this question

How do you solve the system of equations by graphing and then classify the system as consistent or inconsistent $3 x - y = 9$ $3x-y=9$ and $2 x + y = 6$ $2x+y=6$ ?