How do you solve the system of equations by graphing #x+y=3# and #x-y=1# and then classify the system?
1 Answer
Jan 13, 2018
This pair of equations are consistent with a single solution
Explanation:
Graphing solution (sorry I missed this requirement initially.
The graph of
graph{(3-x) [-10, 10, -5, 5]}
and
the graph of
graph{x-1 [-12.66, 12.65, -6.33, 6.33]}
When combined we have
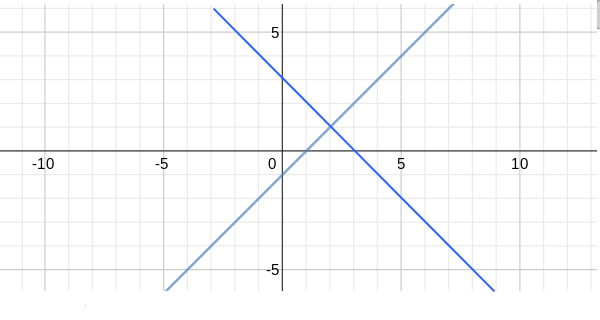
with a single point of intersection at
Non-graphing solution
Given
[1]
[2]
adding [1] and [2] together gives
[3]
which implies
[4]
subtracting [2] from [1] gives
[5]
which implies
[6]
This pair of equations are consistent with a single solution
