Here's the situation
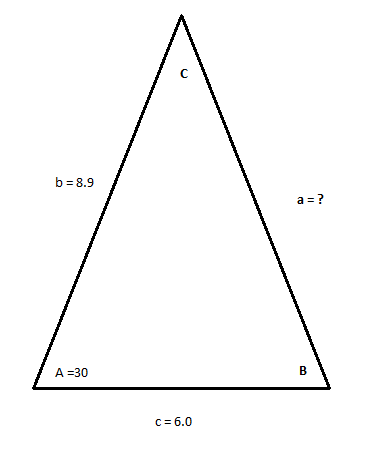
Let's put this in a table:
#color(white)(..)A n g l e color(white)(. . . . ?) | color(white)(..) L e n g t h#
#color(white)(..) A = 30^o color(white)(..?) | color(white)(..) a =?#
#color(white)(..) B = ? color(white)(30^o)color(white)(..) | color(white)(..) b =8.9#
#color(white)(..) C = ? color(white)(30^o)color(white)(..) | color(white)(..) c =6.0#
Law of Cosines
#a^2 = b^2 + c^2 - 2 xx b xx c xx cos(A)#
#a = sqrt( b^2 + c^2 - 2 xx b xx c xx cos(A) )#
#a = sqrt( 8.9^2 + 6^2 - 2 xx 8.9 xx 6 xx cos(30) )#
#a = sqrt( 79.21 + 36 - 92.5 )#
#a = 4.77#
#color(white)(..)A n g l e color(white)(. . . . ?) | color(white)(..) L e n g t h#
#color(white)(..) A = 30^o color(white)(..?) | color(white)(..) a = 4.77#
#color(white)(..) B = ? color(white)(30^o)color(white)(..) | color(white)(..) b =8.9#
#color(white)(..) C = ? color(white)(30^o)color(white)(..) | color(white)(..) c =6.0#
Law of Sine
#sin(A)/a = sin(C)/c#
#sin^(-1)(c xx sin(A)/a) = C#
#sin^(-1)(6.0 xx sin(30)/4.77) = C = 39^o#
#color(white)(..)A n g l e color(white)(. . . . ?) | color(white)(..) L e n g t h#
#color(white)(..) A = 30^o color(white)(..?) | color(white)(..) a = 4.77#
#color(white)(..) B = ? color(white)(30^o)color(white)(..) | color(white)(..) b =8.9#
#color(white)(..) C = 39^o color(white)(..?) | color(white)(..) c =6.0#
Since the angle of a triangle must add up to #180^o#, we already know the angle of #B#:
#180 - 30 - 39 = 111#
#color(white)(..)A n g l e color(white)(. . . . ?1) | color(white)(..) L e n g t h#
#color(white)(..) A = 30^o color(white)(..?1) | color(white)(..) a = 4.77#
#color(white)(..) B = 111^o color(white)(. .?) | color(white)(..) b =8.9#
#color(white)(..) C = 39^o color(white)(. .? 1) | color(white)(..) c =6.0#