How do you solve #x^2+5x+6>0#?
2 Answers
Explanation:
If you struggle to understand any of the steps I made,
feel free to write a comment :)
Range satisfying the given condition:
We can also write the solution using the interval notation as:
Explanation:
Given:
We are given the inequality:
Write this inequality as
Consider the quadratic expression
Split the middle term to factorize as shown below:
We want two numbers that multiply together to make 6, and add up to 5.
Factor the first two terms and the last two terms separately:
Observe that
Hence, we can write our factors as
We will construct the sign chart:
Add
Hence,
Similarly,
We will summarize and create a table of values.

Hence,
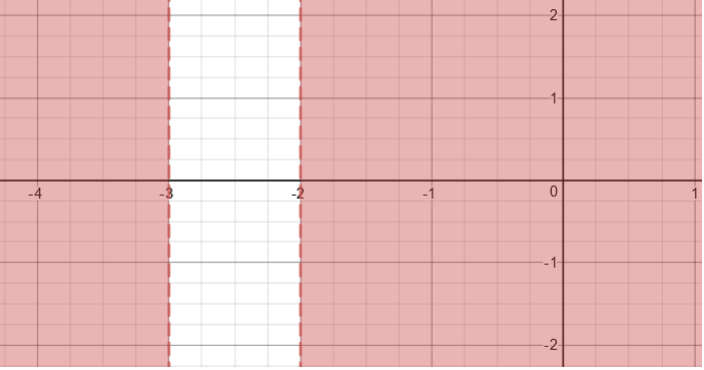
Range satisfying the given condition:
We can also write the solution using the interval notation as:
An image of the graph for the inequality is available below:
Hope it helps.


