By the rational root theorem, a polynomial #qx^n + bx^(n-1) + ... + p#, the possible factors are given by #"factors of p"/"factors of q"# or in our specific case #"factors of 20"/"factors of 1"#. So, we have possible factors of #(+-20, +-10, +- 5, +- 4, +- 2, +-1)/(+-1)#. At the moment, you're probably scratching your head, discouraged, thinking that it will take you forever to find which of the above are factors of our polynomial. Luckily, this is not the case.
There exists the remainder theorem to help us quickly sort out which are viable factors. For a polynomial #f(x) = ax^n + bx^(n - 1) + ... + p#, being divided by #x - a#, the remainder of the division is given by evaluating #f(a)#.
This can be a long process, but generally speaking, you find a factor within the first five tries if you go in increasing order. Starting at 1:
#1^2 + 8(1)^3 + 15(1)^2 - 4(1) - 20 =^? 0#
#24 - 24 = 0#
Hence, #x - 1# is a factor. We need to divide (preferrably by synthetic division) to see the quotient.
#"1_|1 8 15 -4 -20"#
#" 1 9 24 20"#
#"----------------------------"#
#" 1 9 24 20 0"#
So, #(x -1)(x^3 + 9x^2 + 24x + 20) = x^4 + 8x^3 +15x^2 - 4x - 20#
However, since we still have a polynomial of degree #3#, we're going to have to find another factor (if it exists) by repeating the process above. Doing this, you will find that #x + 2# is a factor.
#"-2_|1 9 24 20"#
#" -2 -14 -20"#
#"---------------------------"#
#" 1 7 10 0"#
So, #(x - 1)(x + 2)(x^2 + 7x + 10)# is the factoring
We can factor the trinomial as #(x + 5)(x + 2)#
Hence, #(x - 1)(x + 2)^2(x + 5) > 0#.
Selecting test points for x, you will find that #x< 1# is the solution.
Here is the representation on a) a graph and on b) a number line.
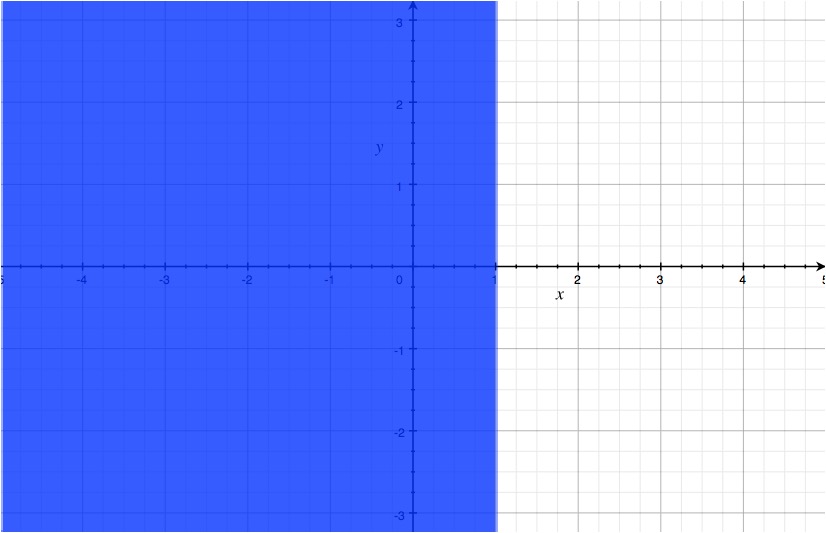
Note: The line should be dotted in the graph (my graphing program cannot do this).

Hopefully this helps!



