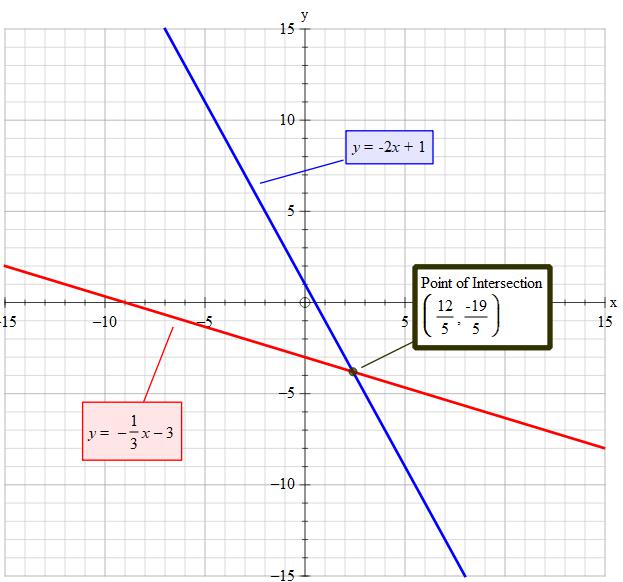
How do you tell whether the system # y= -2x + 1# and #y = -1/3x - 3#has no solution or infinitely many solutions?
2 Answers
If you were to try to find the solution(s) graphically, you would plot both of the equations as straight lines. The solution(s) are where the lines intersect. As these are both straight lines, there would be, at most, one solution. Since the lines are not parallel (the gradients are different), you know that there is a solution. You can find this graphically as just described, or algebraically.
So
See explanation.
Explanation:
The first condition for either no solution or an infinite count of solutions is that they must be parallel.
No solution parallel and different y or x intercepts
Infinite solutions parallel and the same y or x intercept
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Given:
The values in front of the
The red constants at the end are the y-intercepts and they are of different value