Question

How do you use the first and second derivatives to sketch `f(x) = | (x^2) -1 |`?

Answer 1

`f'(x) \ = { (2x-1,,x lt -1), (1-2x,, -1 lt x lt 1), (2x-1,, x gt 1) :}`

`f''(x) = { (2,,x lt -1), (-2,, -1 lt x lt 1), (2,, x gt 1) :}`

Explanation:

Graphing the function will help to answer the question:

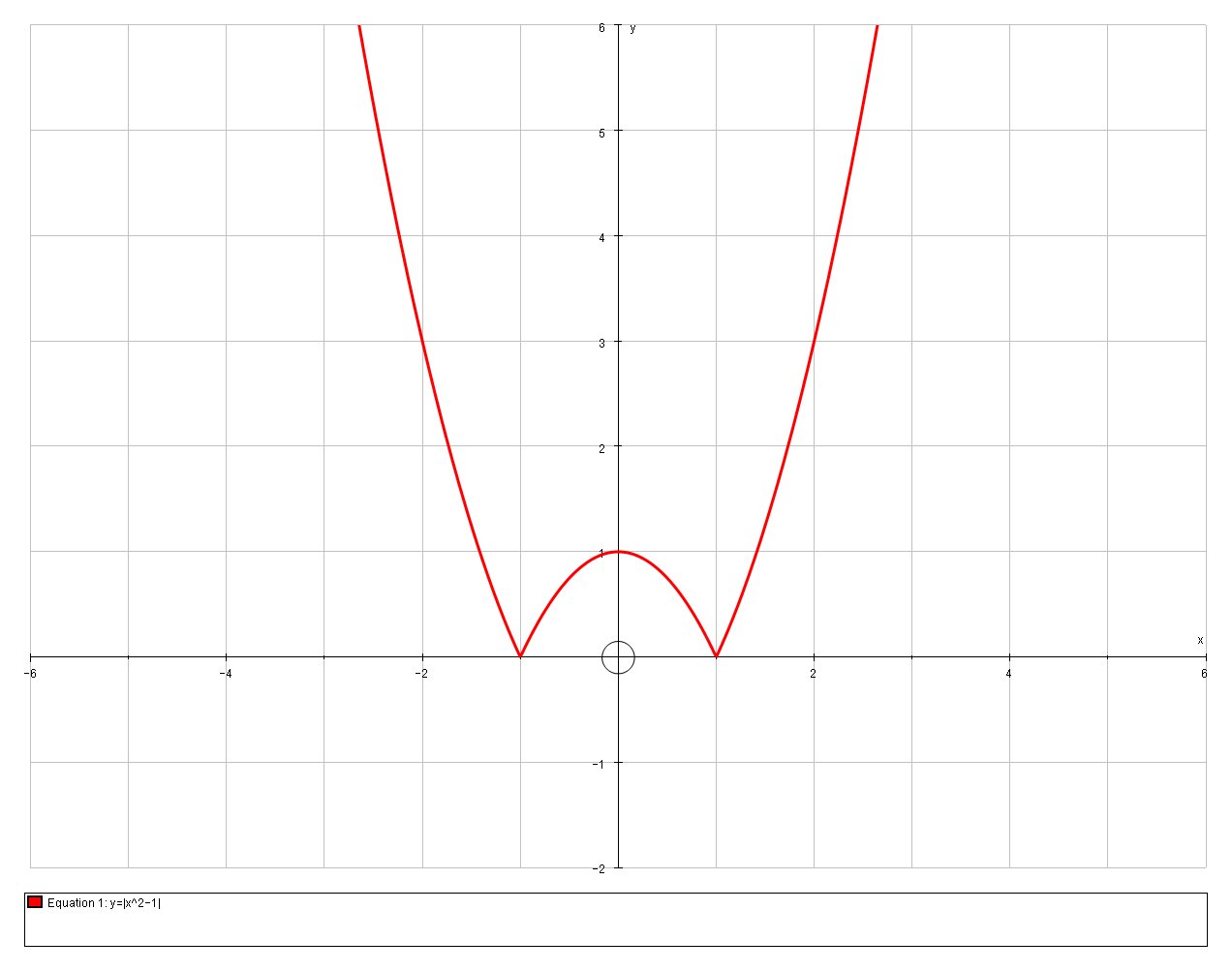
So we can write the function as:

`f(x) = |x^2-1 |`

`" " = { (x^2-1,,x^2-1 gt 0), (-(x^2-1),,x^2-1 lt 0) :}`

`" " = { (x^2-1,,x lt -1), (1-x^2,, -1 lt x lt 1), (x^2-1,, x gt 1) :}`

Note that although `f(x)` is continuous at `x=+-1` the first and second derivatives are not defined at those points.

So then we can easily differentiate to get the first derivative:

`f'(x) \ = { (2x-1,,x lt -1), (1-2x,, -1 lt x lt 1), (2x-1,, x gt 1) :}`

And the second derivative is:

`f''(x) = { (2,,x lt -1), (-2,, -1 lt x lt 1), (2,, x gt 1) :}`