How do you use the first and second derivatives to sketch #f(x)= x^4 - 2x^2 +3#?
1 Answer
The curve is concave downwards at
The curve is concave upwards at
The curve is concave upwards at
Explanation:
Given -
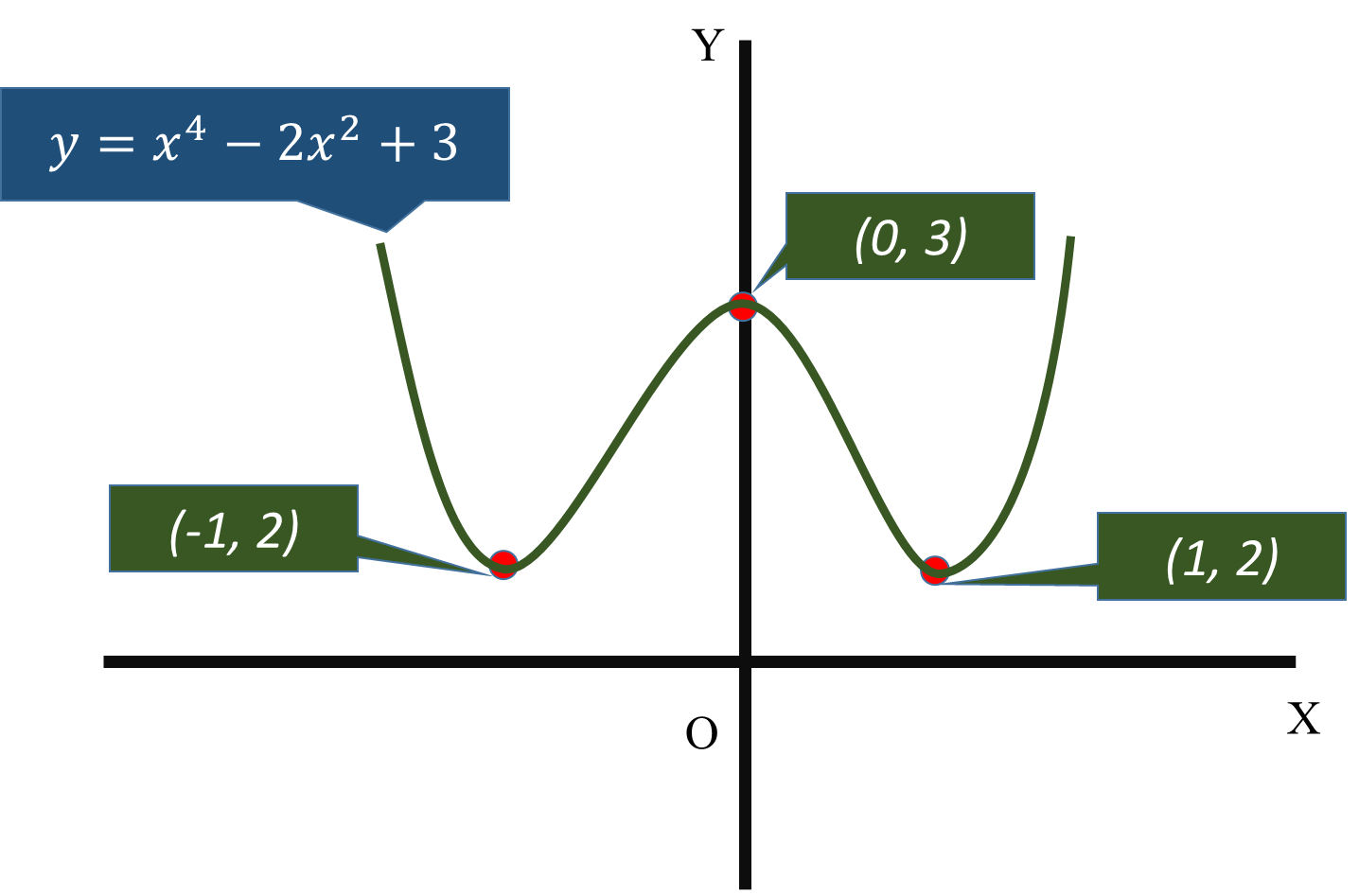
#y=x^4-2x^2+3#
#dy/dx=4x^3-4x#
#(d^2y)/(dx^2)=12x^2-4#
To sketch the graph, we have to find for what values of
#dy/dx=0 =>4x^3-4x=0#
#4x^3-4x=0#
#4x(x^2-1)=0#
#4x=0#
#x=0#
#x^2-1=0#
#x=+-sqrt1#
#x=1#
#x=-1#
The curve turns when
At these points we have to decide whether the curve is concave upwards or concave downwards. For this we need the second derivatives -
At
#(d^2y)/(dx^2)=12(0^2)-4=-4<0#
Since the second derivative is less than zero, the curve is concave downwards at
The value of the function is -
#y=0^4-2*0^2+3=3#
The curve is concave downwards at
At
#(d^2y)/(dx^2)=12(1^2)-4=8>0#
Since the second derivative is greater than zero, the curve is concave upwards at
The value of the function is -
#y=1^4-2*1^2+3=2#
The curve is concave upwards at
At
#(d^2y)/(dx^2)=12(-1^2)-4=8>0#
Since the second derivative is greater than zero, the curve is concave upwards at
The value of the function is -
#y=(-1)^4-2*(-1)^2+3=2#
The curve is concave upwards at