Question

How do you use the first and second derivatives to sketch `h(x)=x³-3x+1`?

Answer 1

First derivative will give us critical points:

Points that represent potential local maximum/minimum values or aymptotes

Plugging in values on either side of these critical points will show how the curve is acting (ie. positive/negative slopes)

Second derivative will give us inflection points:

Points in which the curve changes concavity

...As well as tell us if the curve is concave up/down.

Explanation:

So, lets first take the derivative of `f(x)`

`f'(x) = 3x^2-3`

`f'(x)=0=>3x^2-3=0`

`3x^2=3=>x=+-1` Critical values

Check the intervals around the critical values:

For `(-oo, -1)`, the function is positive `=>`increasing slope

For `(-1, 1)`, the function is negative `=>`decreasing slope

For `(1, oo)`, the function is positive `=>`increasing slope

This should make sense since we started with a cubic function.

These changes in slope indicate local extrema.

Local maximum at `x=-1`
Local minimum at `x=1`

Now, lets take the second derivative:

`f''(x)=6x`

`f''(x)=0=>6x=0`

`x=0`

Check the intervals around this value.

For `(-oo, 0)`, the function is negative `=>` concave down

For `(0, oo)`, the function is positive `=>` concave up

Thus, there is an inflection point at x=0.

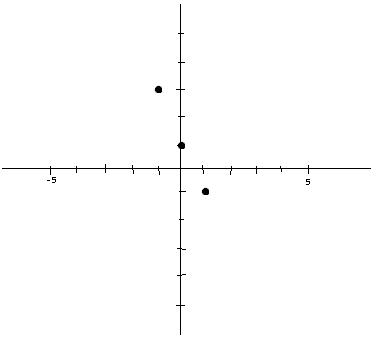
Now that we have all that information, we should gather up some basic information to help us plot.

Let's find some intercepts by plugging in 0 for x into the original function f(x).

`f(0)=0^3-3(0)+1`

y-intercept `=1`

Plug in our extrema values and plot those.

`f(-1)=(-1)^3-3(-1)+1`

`(-1, 3)`

`f(1)=(1)^3-3(1)+1`

`(1, -1)`

Now, we know how the graph acts based on those intervals:

Increasing from `(-oo, -1)&(1, oo)`

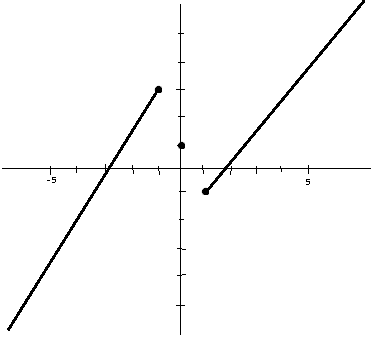
Decreasing from `(-1, 1)`

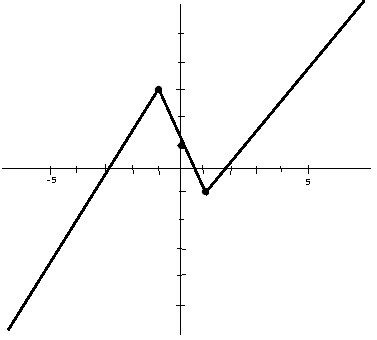
Now concavity; since we know that the function is differentiable along the `RR`

Concave down from `(-oo, 0)`
Concave up from `(0, oo)`

graph{x^3-3x+1 [-5.304, 5.796, -2, 3.546]}