How do you use the first and second derivatives to sketch #y=2x^3- 3x^2 -180x#?
1 Answer
Graph is also available with relevant details.
Explanation:
We are given the function
We will find the First Derivative and set it equal to ZERO.
We will factor out the GCF
This is the First Derivative of
Hence,
We will now set this equal to Zero.
We will split the x-term to get
Roots or Zeros are found at
We can now say that ...
the Critical Numbers in this graph are ( - 5 and 6 )
Let us now place these critical values on a Number Line and then generate a Sign Chart
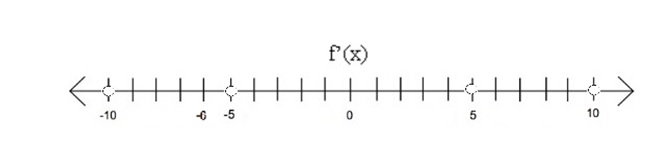
Sign Chart for our First Derivative is given below:

We observe the following for the First Derivative Test:
-
If the first derivative is Positive [ f'(x) > 0 ] then our Original Function is Increasing.
-
If the first derivative is Negative [ f'(x) < 0 ] then our Original Function is Decreasing.
At . .
At . .
We will now find the Second Derivative
We have
We must now find
That is we must differentiate our first derivative
This is our Second Derivative
We will set the Second Derivative Equal to Zero
Critical Point for the second derivative is
Let us now place these values on a Number Line and then generate a Sign Chart
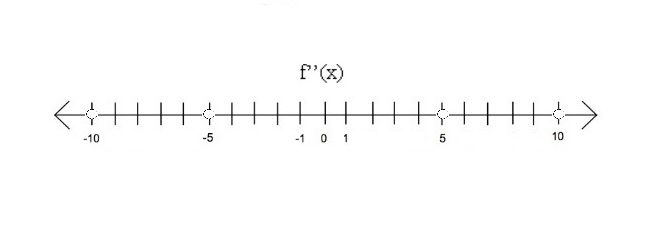
Sign Chart for our Second Derivative is given below:
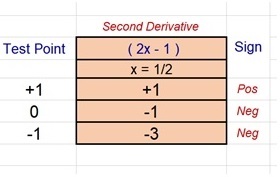
We observe the following for the Second Derivative Test:
-
If the second derivative is Positive [ f'(x) > 0 ] then our Original Function is Concave Up.
-
If the first derivative is Negative [ f'(x) < 0 ] then our Original Function is Concave Down.
The graph below is for the Original Function
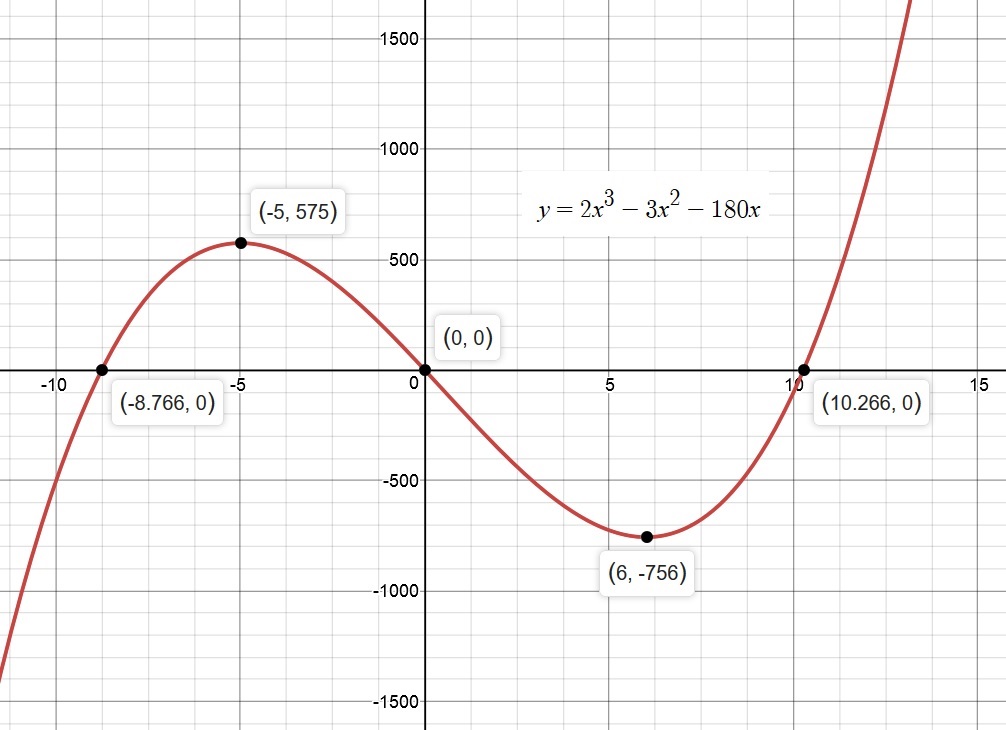
Study the graph and compare the results obtained from the first derivative and the second derivative tests.
Hope this helps.

