How do you use the first and second derivatives to sketch #y = (x+2)(25 -x^2)#?
1 Answer
I got:
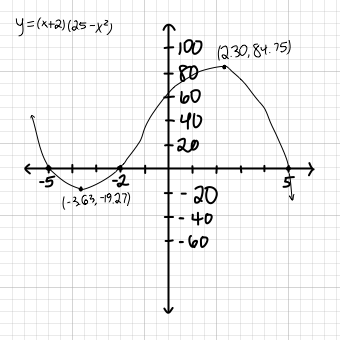
and Socratic graphs show:
graph{(x+2)(25 - x^2) [-8, 6, -107.6, 107.8]}
DISCLAIMER: LONG ANSWER!
To graph this, you need:
- All
#x# intercepts - Coordinates for all extrema
- What these extrema are (maximum or minimum)
GETTING THE X INTERCEPTS
You fortunately have
#color(green)(y) = -(x+2)(x^2 - 25)#
#= color(green)(-(x+2)(x+5)(x-5))# --- difference of two squares
Right now, if you set this equal to
#x = -5# , or#color(blue)("("-5,0")")# #x = -2# , or#color(blue)("("-2,0")")# #x = 5# , or#color(blue)("("5,0")")#
The three roots tell you that there are three
GETTING THE COORDINATES FOR ALL EXTREMA
Now multiply it all out to take the derivatives more easily using the power rule.
#-(x+2)(x^2 - 25)#
#= -(x^3 - 25x + 2x^2 - 50)#
#= -x^3 - 2x^2 + 25x + 50#
Now the first derivative, which gives you where the extrema are, is:
#color(green)((dy)/(dx))#
#= d/(dx)[-3x^2 - 4x + 25]#
#= color(green)(-3x^2 - 4x + 25)#
When you set this equal to
Because you're solving a quadratic, you should get two roots that each tell you where the extrema are. But you don't know whether they are minima or maxima yet. The second derivative tells you that.
Unfortunately this doesn't factor into integer solutions, so we'll have to complete the square.
- Get the
#x^2# term coefficient to be#1# . - Take the resultant
#x# term, halve the coefficient, and square the coefficient to get the#x^0# term. - Make sure you've added the resultant
#x^0# term to both sides.
#-3x^2 - 4x = -25#
#3x^2 + 4x = 25#
#3(x^2 + 4/3x) = 3(25/3)#
#3(x^2 + 4/3x + 4/9) = 3(25/3 + 4/9)#
#3(x + 2/3)^2 = 79/3#
#=> color(green)((dy)/(dx) = 3(x + 2/3)^2 - 79/3 = 0)#
Now, solve this for
#(x+2/3)^2 = 79/9#
#x + 2/3 = pmsqrt(79/9)#
#color(green)(x_1 = sqrt(79/9) - 2/3 ~~ 2.30)#
#color(green)(x_2 = -sqrt(79/9) - 2/3 ~~ -3.63)#
If we plug these in back to the original equation, we can get the coordinates for the extrema.
#color(green)(y_1) = -x_1^3 - 2x_1^2 + 25x_1 + 50 ~~ color(green)(84.75)#
#color(green)(y_2) = -x_2^3 - 2x_2^2 + 25x_2 + 50 ~~ color(green)(-19.27)#
So the two extrema in the graph are:
#color(blue)( "("2.30,84.75")")# #color(blue)( "("-3.63,-19.27")" )#
Now to figure out which one is the maximum and which one is the minimum.
DETERMINING WHETHER THEY'RE MAXIMA OR MINIMA
With the second derivative, we have three options:
- If
#|[(d^2y)/(dx^2)]|_(x = a) > 0# , we have a minimum. - If
#|[(d^2y)/(dx^2)]|_(x = a) < 0# , we have a maximum. - If
#|[(d^2y)/(dx^2)]|_(x = a) = 0# , we have an inflection point, where the concavity changes from concave up to concave down or vice versa.
We have to select the
#color(blue)(|[(d^2y)/(dx^2)]|_(x ~~ 2.30))#
#= d/(dx)[(dy)/(dx)]#
#= d/(dx)[-3x^2 - 4x + 25]#
#= -6x - 4#
#=> -6(2.30) - 4 ~~ color(blue)(-17.78 < 0)#
#=># #\mathbf(color(blue)("maximum"))# (inside of curve faces down)
#color(blue)(|[(d^2y)/(dx^2)]|_(x ~~ -3.63))#
#=> -6(-3.63) - 4 = color(blue)(17.78 > 0)#
#=># #\mathbf(color(blue)("minimum"))# (inside of curve faces up)
There, now we have enough information to sketch this!
GRAPHING THE RESULT
All our coordinates that we just solved for are...
x-intercepts
#(-5,0)# #(-2,0)# #(5,0)#
extrema
#(-3.63, -19.27)# --- minimum#(2.30, 84.75)# --- maximum
So now we graph this as:

and Socratic graphs show:
graph{(x+2)(25 - x^2) [-8, 6, -107.6, 107.8]}

