Question

How do you use the point (9,-5) on the terminal side of the angle to evaluate the six trigonometric functions?

Answer 1

Consider the following diagram:

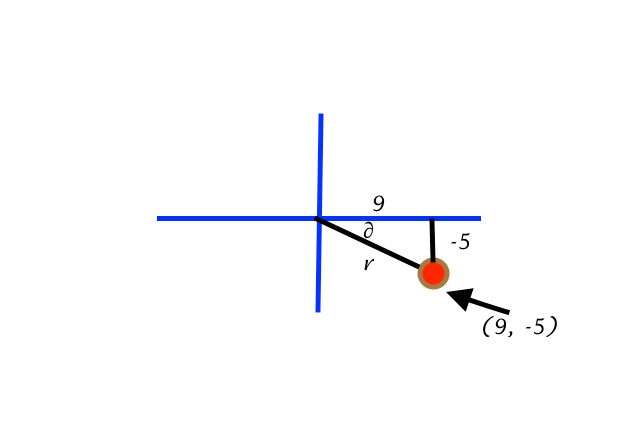
The diagram is just to say that we know the two legs of the triangle, which lie in quadrant four. In other words, we can already state `tanalpha` and `cotalpha`, but to find the other four trigonometric functions we need to know the length of the hypotenuse, or `r`.

We can do this by pythagorean theorem:

`r^2 = (-5)^2 + 9^2`

`r = sqrt(25 + 81)`

`r = sqrt(106)`

Now, we can state the value of all 6 trigonometric ratios.

`sinalpha = "opposite"/"hypotenuse" = -5/sqrt(106) = (-5sqrt(106))/106`

`cscalpha = 1/("opposite"/"hypotenuse") = 1/(-5/(sqrt(106))) = -sqrt(106)/5`

`cosalpha = "adjacent/hypotenuse" = 9/sqrt(106) = (9sqrt(106))/106`

`secalpha = 1/("adjacent"/"hypotenuse") = 1/(9/sqrt(106)) = sqrt(106)/9`

`tanalpha = "opposite"/"adjacent" = -5/9`

`cotalpha = 1/("opposite"/"adjacent") = -9/5`

Hopefully this helps!