Any quadratic function with vertex at #(color(red)(-3),color(blue)(-2))#
can be written in the form:
#color(white)("XXX")y=color(green)m(x-color(red)(""(-3)))^2+color(blue)(""(-2))# for some constant #color(green)m#
or (simplified)
#color(white)("XXX")y=color(green)m(x+3)^2-2#
If #(color(magenta)x,color(brown)y)=(color(magenta)1,color(brown)(14))# is a solution for some specific quadratic with this form:
#color(white)("XXX")color(brown)(14) =color(green)m(color(magenta)1+3)^2-2#
#rarrcolor(white)("XXX")14=16color(green)m-2#
#rarrcolor(white)("XXX")16color(green)m=16#
#rarrcolor(white)("XXX")color(green)m=1#
Given the complete quadratic equation:
#color(white)("XXX")y=color(green)1(x+3)^2-2#
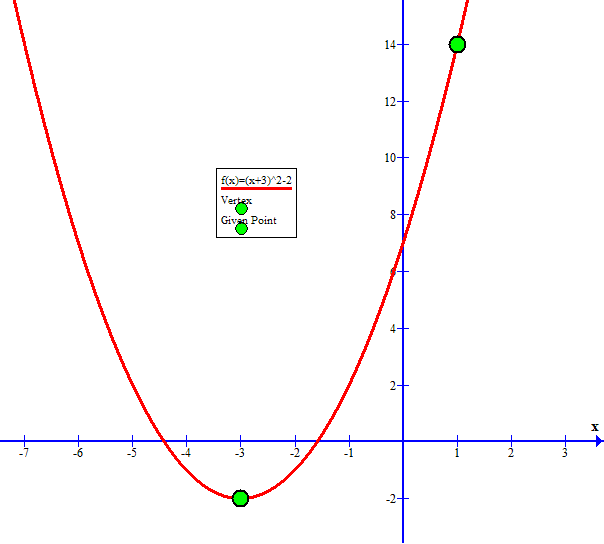
As verification here is the graph of #y=(x+3)^2-2#