How do you write the equation of the parabola in vertex form given vertex (-4,-7) and also passes the point (-3,-4)?
1 Answer
Jan 31, 2017
There are 2 equations, one of the form,
Explanation:
Given the vertex
Using the first form:
Substitute -3 for x and -4 for y:
The first equation is:
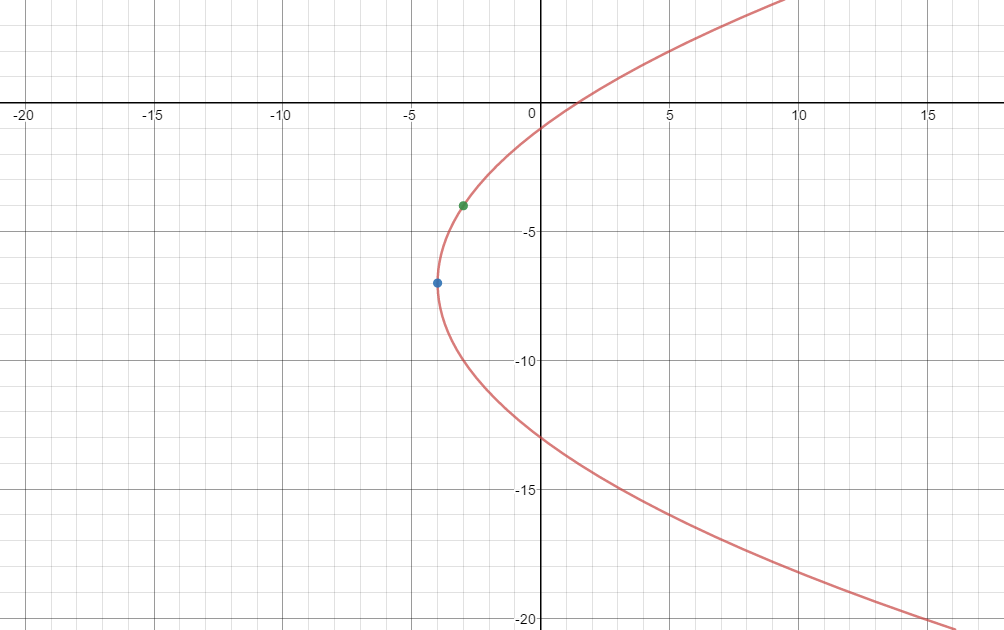
Here is the graph of the equation and the two points:
Using the second form:
Substitute -3 for x and -4 for y:
The second equation is:
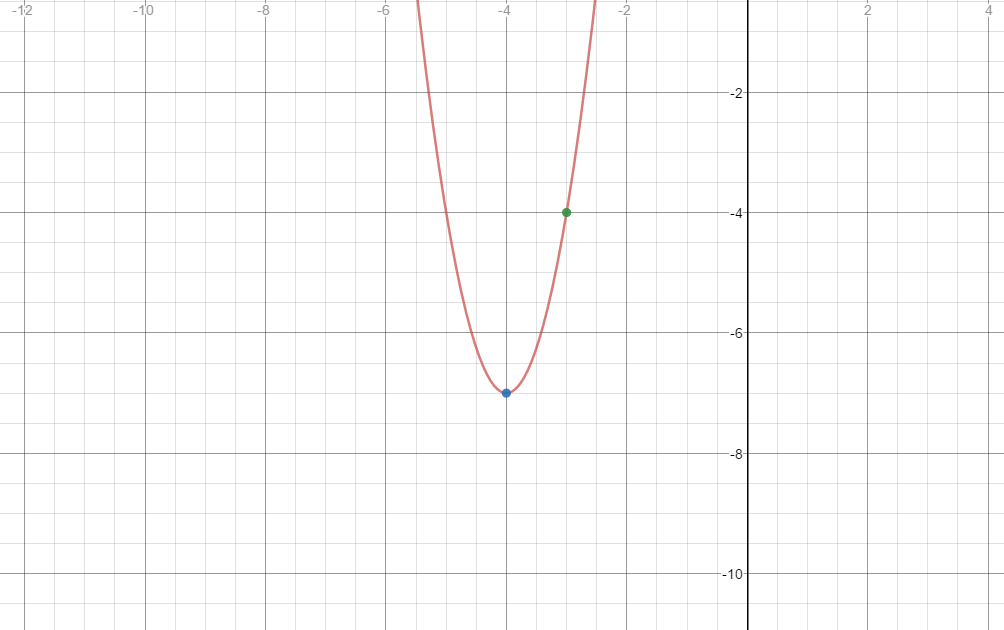
Here is the graph of the equation and the two points: