Question

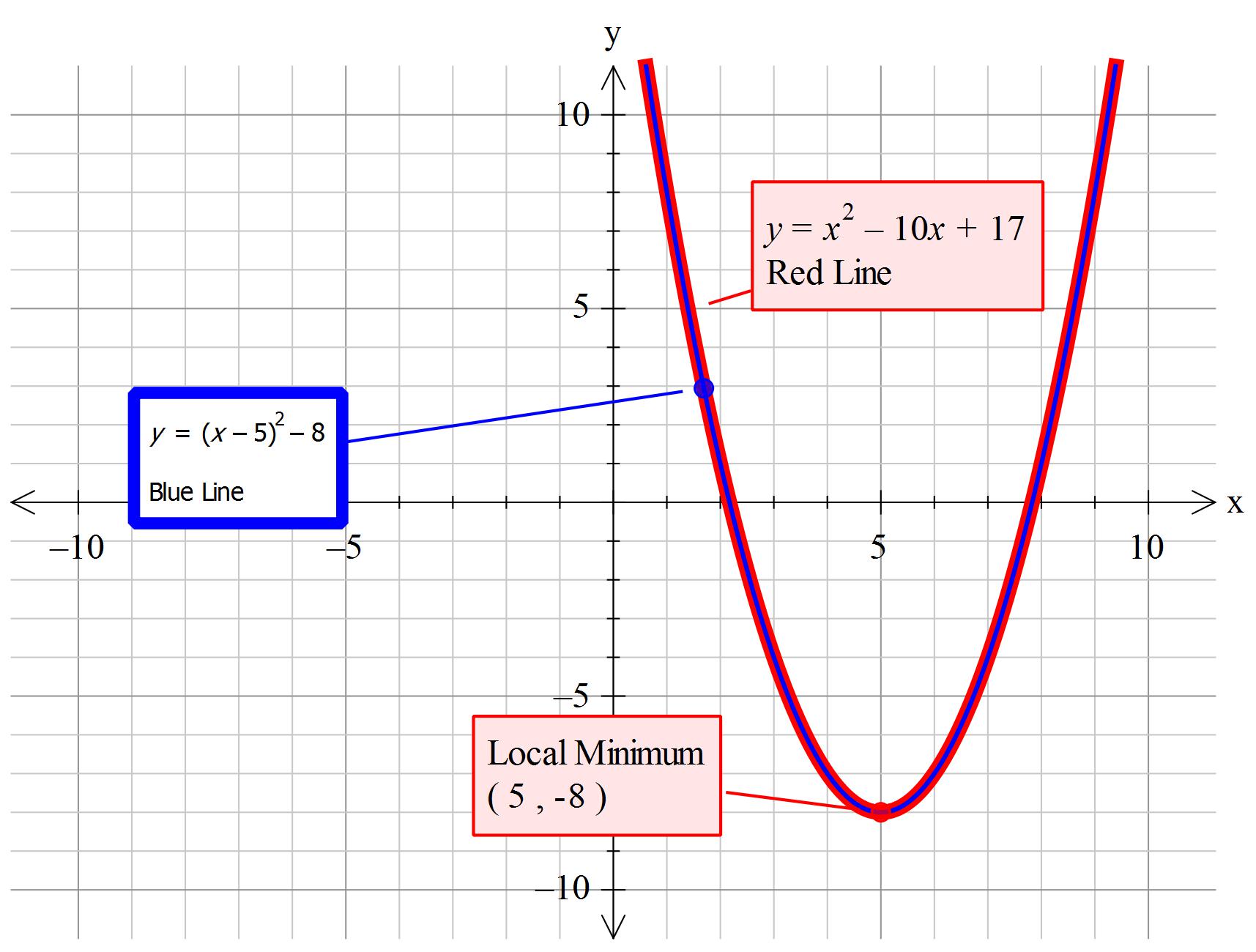
How do you write the Vertex form equation of the parabola `y = x^2 - 10x +17`?

Answer 1

`color(blue)("Vertex form " ->y=(x-5)^2-8)`

Explanation:

This process introduces an error that has to be compensated for
For a really detailed explanation of the process see my solution
http://socratic.org/s/asNAQ6ru

Different values but the method is sound
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let `k` be a corrective constant

Given:`" "y=x^2-10x+17`

Add the corrective constant

`" "y=x^2-10x+k+17`

Insert the first 2 terms into brackets

`y=(x^2-10x)+k+17`

Take the power (index) outside the bracket

`y=(x-10x)^2+k+17`

Apply `(1/2)xx10x` and get rid of the `x`

`y=(x-5)^2+k+17`

'~~~~~~~~~~~~~~~~~~~ Note ~~~~~~~~~~~~~~~~~~~~~~~~~~
The introduced error is from the `(-5)^2=+25` when you square the bracket. So `k=-25`

`" "(x-5)^2 = x^2-10x color(red)(+(-5)^2)`

The `color(red)(+(-5)^2)` is not in the original equation!!!
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`y=(x-5)^2color(red)(-25)+17`

`color(blue)("Vertex form " ->y=(x-5)^2-8)`

`color(magenta)("You can see from the graph that the two equation produce the same plot.")`