Question

How many liters of water can be made from 55 grams of oxygen gas and an excess of hydrogen at a pressure of 12.4 atm and a temperature of 85C?

Answer 1

`"8.2 L"`

Explanation:

Your starting point here will be the balanced chemical equation for the reaction between hydrogen gas and oxygen gas, which looks like this

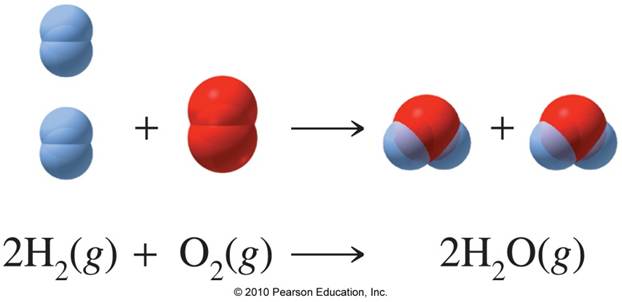
As you can see, you have a `2:1` mole ratio between hydrogen gas and oxygen gas. This means that the reaction will always consumed twice as many moles of hydrogen gas than of oxygen gas.

Likewise, you have a `1:2` mole ratio between oxygen gas and water, which means that the reaction will produce twice as many moles of water as you have moles of oxygen taking part in the reaction.

To find the number of moles of oxygen, use its molar mass

`55 color(red)(cancel(color(black)("g"))) * "1 mole O"_2/(32.0 color(red)(cancel(color(black)("g")))) = "1.719 moles O"_2`

You are told that hydrogen is in excess, which means that you can assume that all the moles of oxygen will react.

This means that the reaction will produce

`1.719 color(red)(cancel(color(black)("moles O"_2))) * ("2 moles H"_2"O")/(1 color(red)(cancel(color(black)("mole O"_2)))) = "3.438 moles H"_2"O"`

To determine what volume that many moles of water would occupy at a pressure of `"12.4 atm"` and a temperature of `85^@"C"`, you can use the ideal gas law equation

`color(blue)(PV = nRT)`

The value of `R`, the universal gas constant, is usually given as `0.0821("atm" * "L")/("mol" * "K")`. Do not forget to convert the temperature from degrees Celsius to Kelvin!

Rearrange the above equation to solve for `V`

`PV = nRT implies V = (nRT)/P`

`V = (3.438color(red)(cancel(color(black)("moles"))) * 0.0821(color(red)(cancel(color(black)("atm"))) * "L")/(color(red)(cancel(color(black)("mol"))) * color(red)(cancel(color(black)("K")))) * (273.15 + 85)color(red)(cancel(color(black)("K"))))/(12.4color(red)(cancel(color(black)("atm"))))`

`V = "8.153 L"`

Rounded to two sig figs, the number of sig figs you have for the mass of oxygen, the answer will be

`V = color(green)("8.2 L")`