How would you identify the period, block and group of the element with the electron configuration #[Ar]3d^7 4s^2#?
1 Answer
#"n" = 4# #"d"# -block- Group
#9# or equivalently group#"VIII (B)"#
Explanation:
The symbol
On the top of that, a ground-state atom of this element would contain valence electrons
The block on the periodic table an element belongs to is dependent on the type of the occupied electron orbital of highest potential energy.
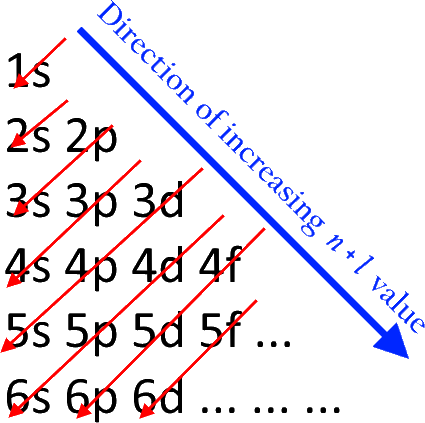
Referring to the Aufbau Diagram above, the electron of the highest potential energy in a ground-state atom of this element lies in a
An atom of this element contains
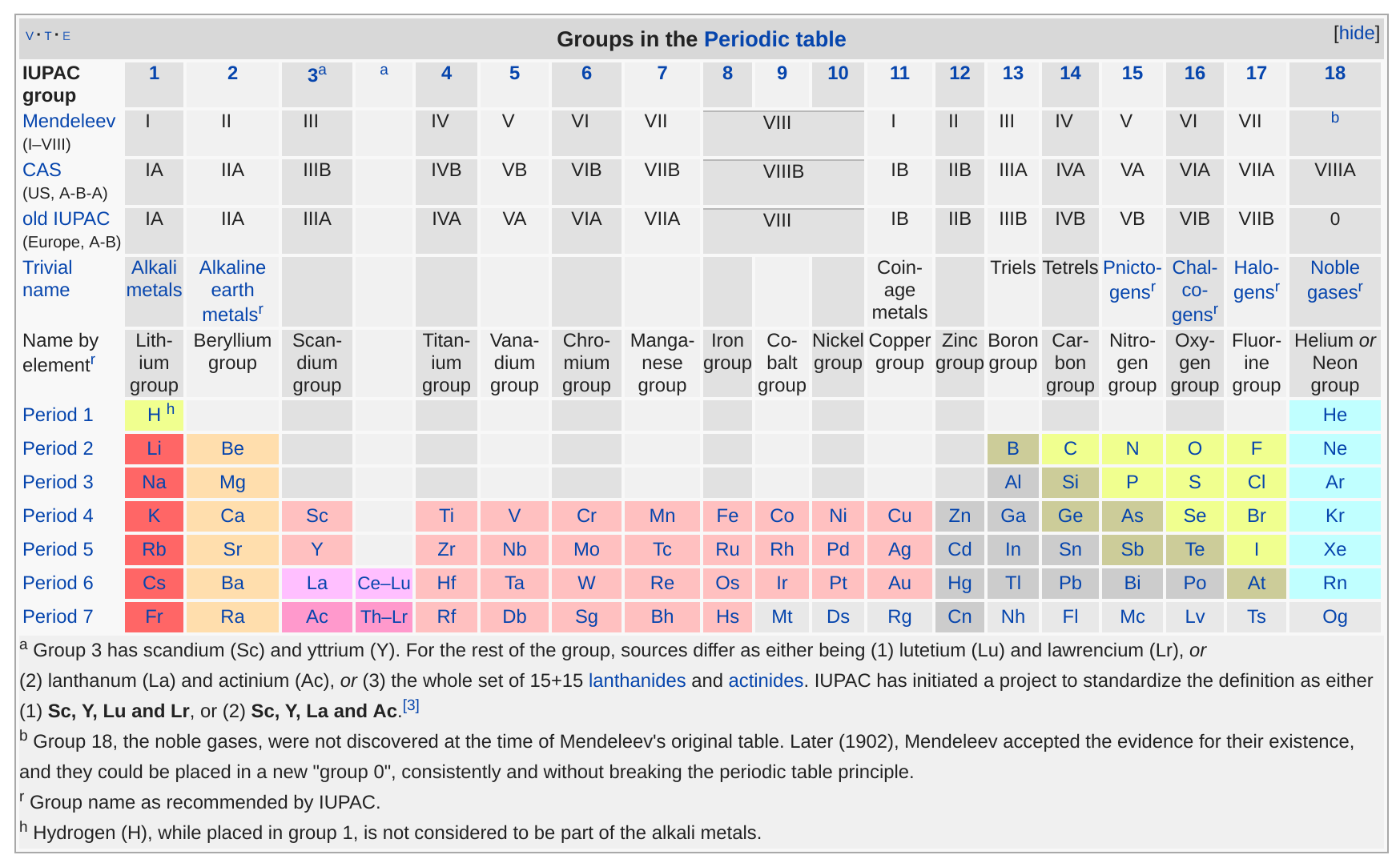
References:
"Group (periodic table)", English Wikipedia, https://en.wikipedia.org/wiki/Group_(periodic_table)
"Block (periodic table)", English Wikipedia,
https://en.wikipedia.org/wiki/Block_(periodic_table)

