I am very confused about anti-bonding orbitals, how they form? I mean when two atomic orbitals produce bonding orbital + anti-banding orbital?? Please clear my basics. I am really worried, please solve my problem
3 Answers
Both the antibonding orbitals and the bonding ones are obtained in the same way and in the same operation: when the AOs are combined to obtain the MOs.
Explanation:
When the combination of two atomic orbitals is generated to obtain molecular orbitals, the most common procedure is to use the LCAO method.
That means that we are going to do a linear combination of two wave functions (the AOs) and that, therefore, we will get two new wave functions (the MOs). One such combination stabilizes the electrons, while the other gives rise to a higher energy.
Therefore, the first will be a bonding orbital, i.e. a molecular orbital in which the electrons will have an energy less than the sum of the energies they had in the separated AOs. In contrast, the second MO obtained will be the antibonding orbital, in which the electrons will have an energy greater than the sum of the energies that they had separately.
You should consider the adjectives "bonding" and "antibonding" as descriptive of the energy levels of the electrons that will occupy those molecular orbitals. That is, an antibonding orbital is not an esoteric concept, but only a molecular orbital whose energy level is above the energy levels of the atomic orbitals from which it comes. A molecule, in its ground state, will always first fill the bonding orbitals of each energy level before occupying the antibonding.
Antibonding orbitals form upon out-of-phase orbital overlap, which is destructive interference. They always form alongside bonding orbitals, due to conservation of atomic orbitals. But, they are not always occupied.
A new node forms between the antibonding orbitals, a region in which electrons cannot be. That limits the regions where the electrons can be, which increases electron repulsion and makes antibonding orbitals higher in energy than the corresponding bonding orbital.
The nodes (nodal planes) are in between where the orbital lobes are opposite in sign (opposite shading):
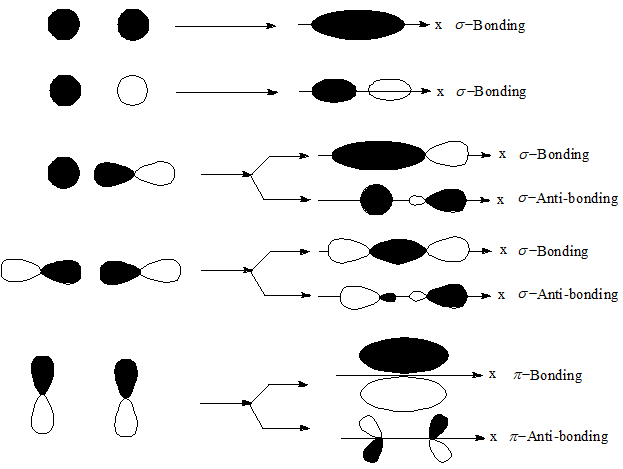
(Note that a bonding orbital can have nodes.)
MOs are defined like a linear combination of AOs, i.e.:
where
Explanation:
Since Newton's time we know that when we have a system with more than two particles interacting with each other by central forces, there is no exact analytical solution of the equations of the motion of these particles. In this context is known the old problem of the movement of three bodies subjected to gravitational interactions between them, which was soon found to have no exact mathematical solution.
In the specific case of the study of the atomic and molecular structure, where the electrostatic interactions predominate, the Schrödinger equation for a monoelectronic atom has an exact solution. It would be the case of the hydrogen atom and the hydrogen like atoms (atoms with
However, if we are talking about polyelectronic atoms or molecules, this equation is not separable in any coordinate system, which makes it non-integrable and we can not solve it exactly. That forces us to look for approximate methods. The two most important families of methods are:
- Variations methods.
- Perturbation methods.
There are different ways of implementing these methods, with MO theory being one of the most useful in describing electronic and magnetic properties of molecules, as well as the study of different types of reaction mechanisms in many chemical reactions.
The theory of molecular orbitals starts from the idea of considering that electrons are not assigned to individual bonds between atoms (as for example in valence bond theory, VB ), but that their movement is influenced by the nuclei of the whole molecule . In this theoretical model, each molecule has its electrons distributed in a series of orbitals, which we shall call molecular orbitals, analogously to the case of individual atoms, which describe the movement of their electrons by atomic orbitals.
We start from the following postulates:
1) Molecular orbitals are mathematically defined as a linear combination of atomic orbitals :
2) A molecular orbital is complete if it contains two electrons.
The Pauli exclusion principle is applicable to molecular orbitals since any wave function describing the motion of an electron must meet the property of being antisymmetric since electrons are fermions. Therefore, in the same orbital, two electrons with identical wave functions can not coexist. This implies that, in keeping with the remaining quantum numbers, we must at least have the spin quantum number different, as in atomic orbitals, and therefore we can only accommodate two electrons in each orbital.
3) The linear combination of a given number of atomic orbitals gives the same number of molecular orbitals.
In formula [eq 1] we can see that both
From a mathematical point of view, we will say that the
4) Half of the molecular orbitals obtained by combining atomic orbitals of the same or similar energy are more stabilized (have less energy) than these and we will call them bonding. The other half are called anti-bonding and have more energy than the atomic orbitals from which they come. They are usually represented by adding an asterisk (
5) The MOs obtained by a linear combination of atomic orbitals that are symmetrical with respect to the bond axis (the orbitals
The MOs obtained by combining atomic orbitals that have a nodal plane on the bond axis, retain this same nodal plane and are called
6) The progressive occupation of MOs follows the same rules as that of atomic orbitals.
Example:
Let's look at a qualitative example explaining the electronic structure of the nitric oxide, NO, molecule.
The electronic configurations of the nitrogen and oxygen atoms are:
In the energy diagram below you can see (there is no scale, it is a qualitative diagram) that we have five atomic orbitals for each atom of the molecule. I.e., both on the part of nitrogen and on the part of oxygen, we have the orbitals
It should be noted that oxygen energy levels are slightly below nitrogen levels because, as the nuclear charge is higher and it is a more electronegative element, the oxygen electrons receive a greater attraction by the nucleus and, therefore, their orbits would be closer to this, being somewhat more stable (less energy) than those of nitrogen. When we have equal atoms, of course, the energy levels of the atomic orbitals that are combined are the same.
Therefore, we will have to combine five atomic nitrogen orbitals with five atomic oxygen orbitals. That means we will get ten molecular orbitals for the NO molecule.
In principle, we should make each molecular orbital a linear combination of these ten atomic orbitals, but it seems reasonable to admit that the inclusion of those atomic orbitals having very different energies from the mean value for the resulting molecular orbital will generate very small coefficients. In other words, as atomic orbitals have energy levels that are increasingly distant from the energy level of the molecular orbital we are calculating, the weight of these orbitals in the linear combination decreases. This allows us to neglect all these contributions so that we will only consider those linear combinations of atomic orbitals whose energy is the same or very similar.
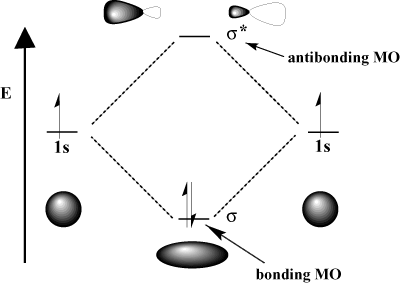
Applying this to the molecule of the example, the result is the energy diagram shown in the drawing above. The nitrogen 1s orbital we will combine linearly with the 1s orbital of the oxygen and that will generate us two molecular orbitals type σ, the bonding and the antibonding. The bonding MO will have less energy than the original two orbitals, while the antibonding MO will have higher energy.
In the diagram below we can see the energy differences mentioned above as well as other types of molecular orbitals that appear when the wave function of an atomic orbital of some of the atoms does not have adequate symmetry to be combined linearly with any of the Wave functions of the remaining atoms of the molecule. In this case, the atomic orbital will generate a molecular orbital practically identical to him and with very similar energy. This molecular orbital is called nonbonding.