Question

If an asteroid has a perihelion distance of 2.0 A.U. and an aphelion distance of 6.0 A.U., what is its orbital semi-major axis, eccentricity, and period? Thanks!?

Answer 1

`a=4.0"AU"`,
`e = .5`,
`T=2"years"`

Explanation:

http://hyperphysics.phy-astr.gsu.edu/hbase/kepler.html

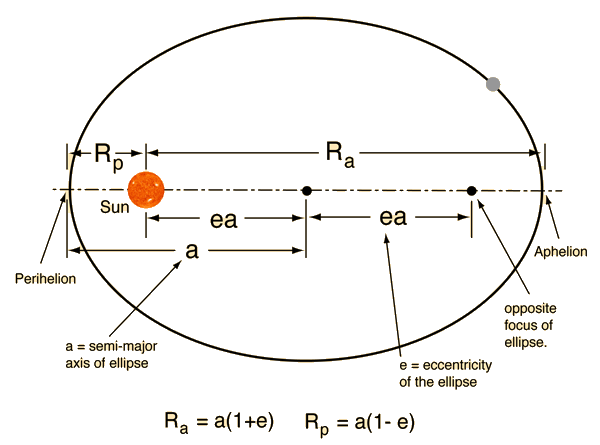
The semi-major axis, `a` of and ellipse is half of the major axis, the total distance between perihelion and aphelion. The semi-major axis is therefore equal to;

`a = (R_a + R_p)/2 = (6.0"AU"+2.0"AU")/2 = 4.0"AU"`

Eccentricity is defined as the ratio of the distance between two focus of the ellipse, `R_a - R_p`, and the length of the major axis, `R_a + R_p`. This can be expressed mathematically as;

`e = (R_a - R_p)/(R_a + R_p) = (6.0"AU" - 2.0"AU")/(6.0"AU"+2.0"AU")=.5`

The period, `T`, can be found using the Kepler's 3rd law, which states that the ratio of the period squared to the semi-major axis cubed is a constant for all objects orbiting the same body. In other words, for two objects that orbit the sun;

`T_1^2/a_1^3 = T_2^2/a_2^3 = C`

Or, restated;

`T_1^2 = a_1^3/a_2^3 T_2^2`

If we use the Earth as object `2`, then `T_2` and `a_2` are both `1`. We can calculate the period of the asteroid using its semi-major axis, `a=4.0"AU"`.

`T_1^2 = (4.0"AU")^3/(1"AU")^3 (1"year")^2 = 4.0"years"^2`

Taking the square root, we get a period of `2"years"` for the asteroid.