In a right- angled triangle, the shortest sides are 5 and 12. How do you find the perimeter of the triangle?
1 Answer
May 23, 2018
The perimeter of the triangle is 30 units.
Explanation:
You have to use the "Pythagorean theorem " in order to find the greatest side / Hypotenuse of the triangle .
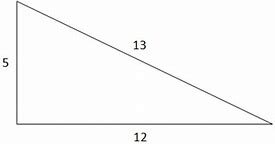
Pythagorean theorem states that - " The sum of the squares of the smaller sides of a right angled triangle is equal to the square of the greatest side / hypotenuse of right angled triangle ".
Let the third side be 'x'
So ,
The greatest side / hypotenuse of the triangle = 13
The perimeter of a triangle = Sum of all sides

