In a right triangle ABC, right angled at B, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. How do you prove that the tangent to the circle at P bisects BC?
1 Answer
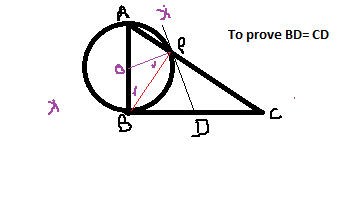
The required proof would be to prove that points B,P and D lie on a semicircle with centre D.
Explanation:
OB= OP , radii of the given circle. Hence angle OBP= angle OPB.
angle OPD is a rt angle ( PD is a tangent). Hence angle BPD= 90-OPB. Similarly, angle PBD= 90- angle OBP. Since OBP and OPB ar equal, angle BPD= angle PBD and therefore DB=DP.
Next, angle OPX is rt. angle and angle APX= angleDPC, hence angle BPC= Angle BPD+angle APX
Since, angle APX +APO =90 and also APO +OPB=90,this means APX=OPB.
Hence angle BPC = Angle BPD +angle APX = Angle BPD +angle OPB = angle OPD =90
BPC is therefor a right triangle and BC is a diameter. Since DB=DP, and D lies on the diameter, BD would be equal to CD.
****
