The area under the curve y=e^-x between x=0 and x=1 is rotated about the x axis find the volume?
1 Answer
Apr 10, 2018
Volume is
Explanation:
Let us see the graph of
graph{e^(-x) [-2.083, 2.917, -0.85, 1.65]}
To find the desired volume the shaded portion (shown below, will have to be rotated around
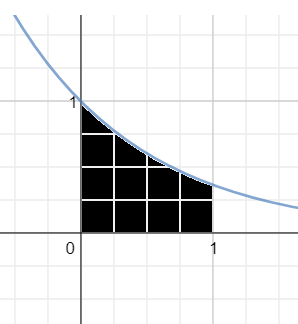
As volume of a cylinder is
and hence volume would be
=
=
=
=
=
=
