Question

What are the components of the vector between the origin and the polar coordinate `(1, (11pi)/6)`?

Answer 1

`((sqrt3/2),(-1/2))`

Explanation:

Convert Polar to Cartesian coordinates using the formulae that link them.

`color(red)(|bar(ul(color(white)(a/a)color(black)( x = rcostheta , y = rsintheta)color(white)(a/a)|)))`

now `(11pi)/6" is an angle in the 4th quadrant "`

where the cos ratio has a positive value and the sin ratio a negative value.

The 'related' acute angle is `(2pi-(11pi)/6)=pi/6`

so `cos((11pi)/6)=cos(pi/6)`
and `sin((11pi)/6)=-sin(pi/6)`

Using the `color(blue)" Exact value triangle for this angle "`

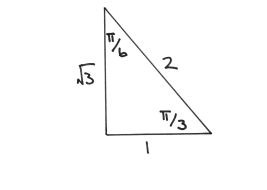
here r = 1 and `theta=pi/6`

`rArr x=rcostheta=1xxcos(pi/6)=sqrt3/2`

and `y=-rsintheta=1xx-sin(pi/6)=-1/2`