What are the components of the vector between the origin and the polar coordinate #(1, (5pi)/4)#?
1 Answer
Jan 15, 2016
The
The
Explanation:
Remembering our trigonometry, the vertical component of a vector is given by
and the horizontal component by
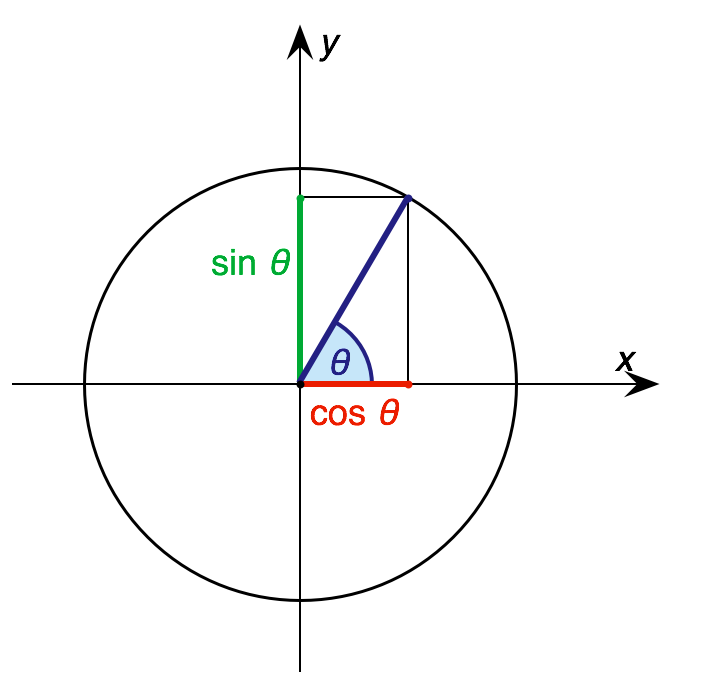
in the polar coordinate
Hence:
The
The
In this case,
