A radiator contains 10 quarts of 30% of which is antifreeze. How much fluid should be drained and replaced with pure antifreeze so that the new mixture 40% antitreeze?
2 Answers
Explanation:
Current amount of antifreeze in quarts is
Target is
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let the amount drained of and replaced with pure antifreeze be
The amount left after draining off is
The amount of antifreeze in this is
The replacement is pure antifreeze which is the amount
so
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Different approach
Drain off and replace
Explanation:
This is a very effective method
You are blending two liquid with different concentration of antifreeze. One liquid has 30% concentration and the other 100% concentration.
If you have all of the original the antifreeze is 30%. If you have all the other the antifreeze content is 100%.
Connect the two points on a graph and you have a model for those conditions and all the other blend concentrations in between. From this we can and may determine the blend that gives us 40%. Sometimes it takes a little thought about how so set up the x-axis which represents the quantities of the blend.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
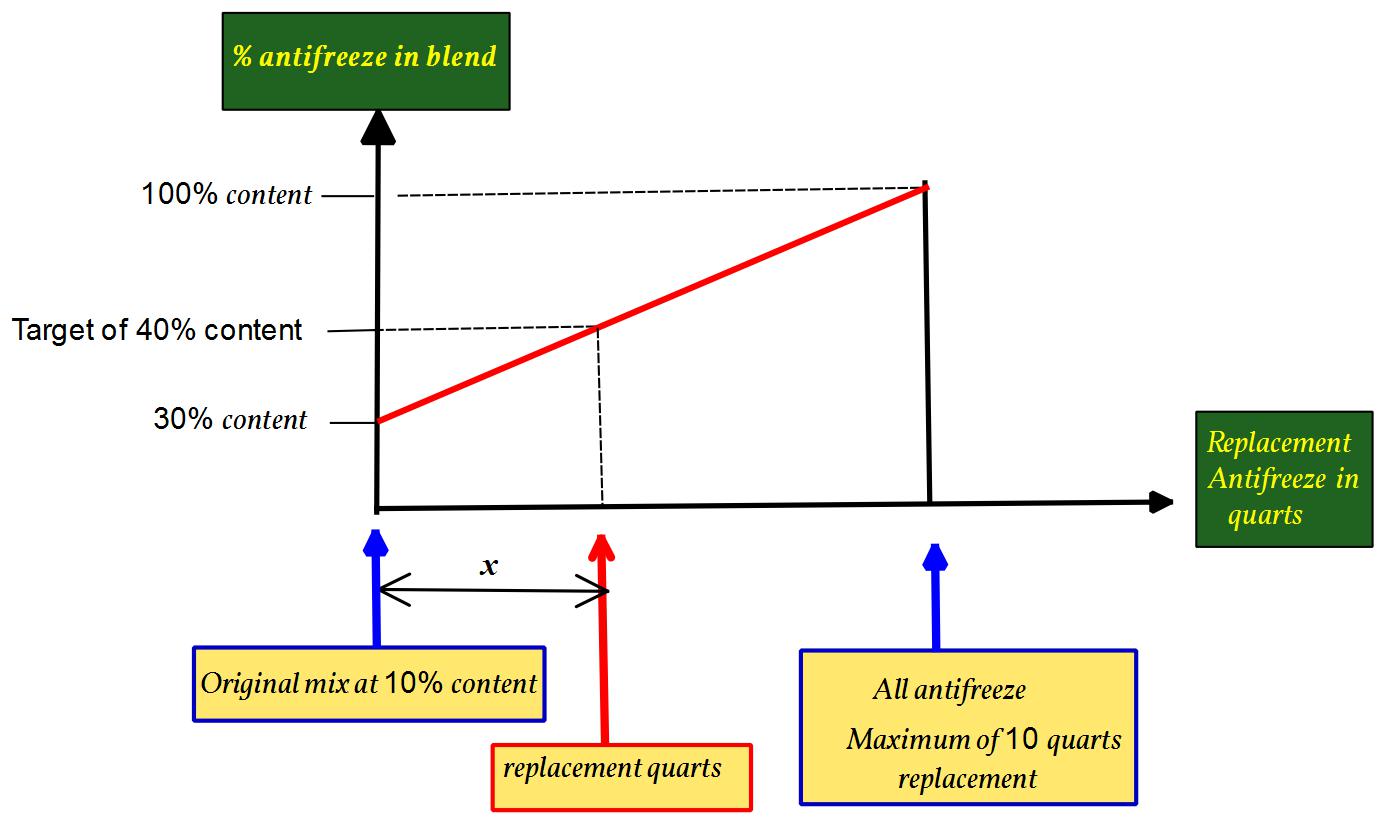
The slope of part of the graph is the same as the slope of all of it.
As we need

