What is the antiderivative of #xsqrtx#?
2 Answers
Jul 27, 2015
You can simply multiply them together (more explicitly).
And then just use the reverse Power Rule.
Then, since an antiderivative is a generalization of what an integral does, they are almost the same thing. Therefore, we add a constant to imply that you get every single function that is within the antiderivative's slope field.
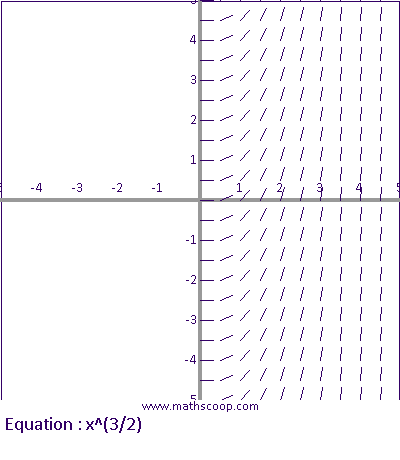
(notice the various vertical-shift variations of a single function forms the slope field)
Jul 27, 2015
Explanation:
Note :
Therefore,

