What is the orthocenter of a triangle with corners at #(4 ,5 )#, #(8 ,3 )#, and (7 ,9 )#?
1 Answer
Coordinates of orthocenter
Explanation:
Orthocenter is the intersection point of the three altitudes of a triangle
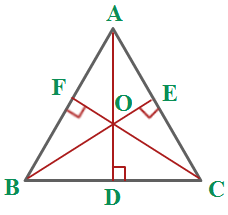
Slope of BC
Slope of (AD) altitude passing through point
Eqn of (AD) Altitude through point A is
Slope of AC
Slope of (BE) altitude passing through point B
Eqn of (BE) Altitude passing through point B is
Solving Eqns (1), (2) we get the orthocenter coordinates.
Coordinates of orthocenter (56/11, 57/11)
This can be verified by solving the third altitude passing through point C as all the three altitudes intersect at the orthocenter.
