What is the shape of the graph #r^2= - cos theta#?
2 Answers
Correcting an error.
Explanation:
This graph is for
with
See the attached plot.
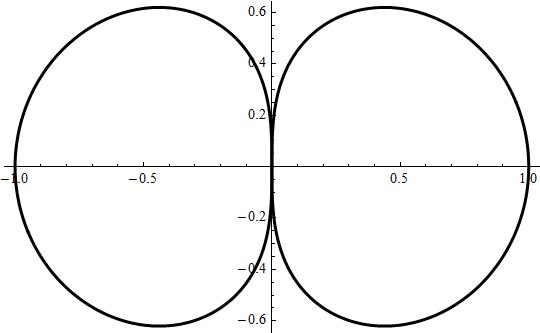
See explanation for the loop.
Explanation:
As
the initial line
I strictly stick to the definition of (length) r as non-negative.
The Table for plotting the graph is
Symmetry about the axis
half of the loop.
Note that I have considered only one loop from
and did not consider the non-positive
for the opposite loop, for the same
My r is a single-valued function of

