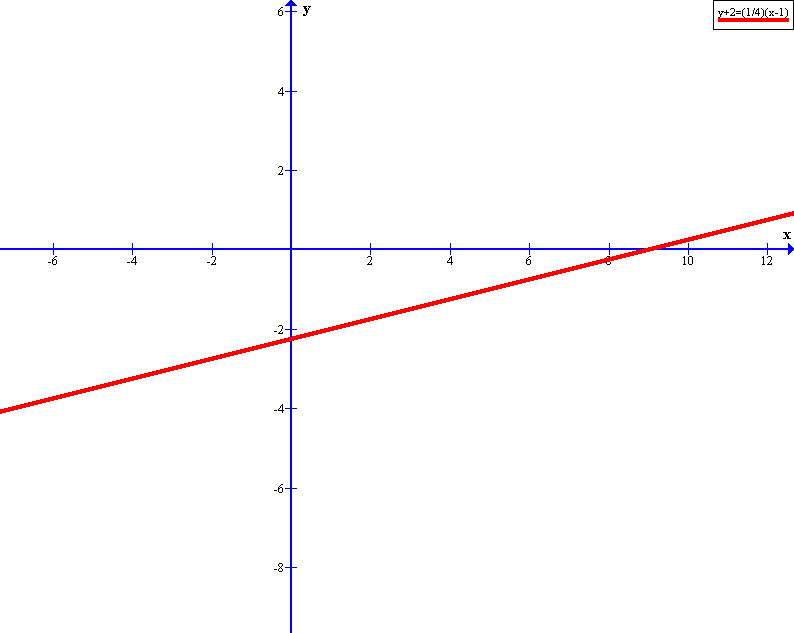What is the slope and intercept for #y+2=1/4(x-1)#?
2 Answers
We'll have to get this into a
Explanation:
Subtract
Now, lose the brackets:
Or:
Where
graph{0.25x-2.25 [-6.83, 13.17, -6.76, 3.24]}
Slope:
Explanation:
Remember that the general slope-intercept form is
with slope of
Given
we wish to convert this into slope-intercept form.
So this line has a slope of
and a y-intercept of