How were the shapes of s, p, d, and f orbitals determined? How did they get their names of s, p, d, and f?
1 Answer
The orbital shapes are actually representation of
Orbitals are actually bounded regions which describe an area where the electron can be .Probability density of an electron is the same as
The wave function
where
harmonic.
For the hydrogen atom wavefunctions for different quantum values(which can be assigned to different orbitals are )

We know that for a 1s orbital in the hydrogen atom
Therefore the the wavefunction is given by
The wavefunction of the 1s orbital doesn't has a angular component and that can be easily figured out by the equation describing it.
Because angular component Y is dependent on
For some equations you may see the angular part like
If you want a single function to describe all orbitals for the hydrogen atom then
If r here approaches
Different quantum numbers

I'll not go into this but all this can be deviated from the Schrodinger equation for the hydrogen atom (for this image)
Now when we know why the wavefunction is different for each orbital you can now analyze the plots
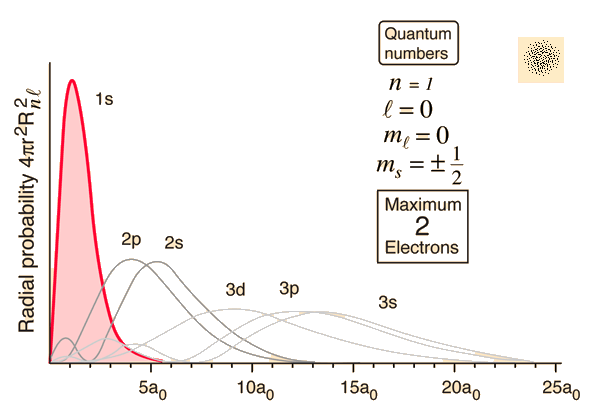
Now there are some ups and down in the plot which are caused by nodes
What are nodes?
Wavefunctions are the solutions to the TISE. Mathematically these differential equations create the nodes in the bound state wave functions, or orbitals. Nodes are the region where the electron probability density is 0.The two types of nodes are angular and radial.
Radial nodes occur where the radial component is 0

Angular nodes are either x, y, and z planes where electrons aren’t present while radial nodes are sections of these axes that are closed off to electrons.

As total number of nodes =
Apart from this there is another method to calculate it but then you have the separate the TISE for hydrogen atom in angular and radial component which is very useful while proving this statement
.
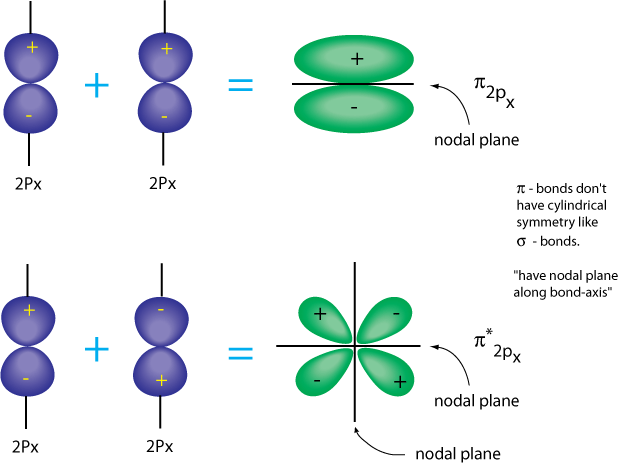
Dotted clouds
It is easier to visualize an orbital with dotted clouds
Sometimes negative and positive signs are used to describe the probability density of an electron in a pi orbital
Naming of the orbitals
They are derived from the description by early spectroscopists of certain series of alkali metal spectroscopic lines as sharp,
principal, diffuse, and fundamental. It has nothing to do with the orbitals.


