Question

Why is a staggered conformer more stable than an eclipsed conformer?

Answer 1

A staggered conformer is more stable than an eclipsed conformer as the latter involves unfavourable energy interactions between atoms.

In conformational analysis (energetics study of different rotational conformers or rotamers), structures are represented by *Newman projection * (atoms and bonds are viewed along the axis of rotation ).

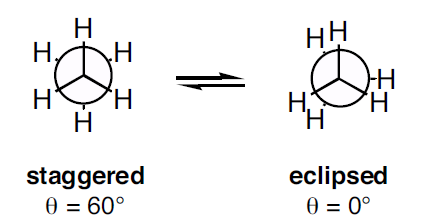
If we consider ethane as a reference molecule for our conformational analysis and check their Newman projection we can easily see the two extremes. The staggered conformation with the dihedral angle of `60^o`, where the H atoms on the 1st carbon are at maximum separation from H atoms on the 2nd carbon. In contrast stands the eclipsed conformation where the H atoms line up perfectly!

However, this perfectly lined up orientation is energetically unfavourable as the negative charged electrons in the bond repel each other strongly. This is why staggered conformation is more stable.