Introduction to Newman Projections
Key Questions
-
Sawhorse projections generally show when something is antiperiplanar or synperiplanar, more easily than something like a Newman projection or a basic line structure can.
Take ethane as an example.
An antiperiplanar conformation has a
180^@ dihedral angle, i.e. the atoms of interest across one bond are on opposite sides along the vertical molecular plane.A synperiplanar conformation has a
0^@ dihedral angle, i.e. the atoms of interest across one bond are on the same side along the vertical molecular plane.A sawhorse projection approximates this 3D structure extremely well, and allows one to judge whether an
E2 reaction is likely to occur or not (it requires an antiperiplanar conformation).A Newman projection would depict the dihedral angle correctly, but because one would be viewing the important atoms from the front instead of an aerial view, you might actually be looking at an octahedral molecule (with a main-chain bond length of
0 ), instead of, say, a two-carbon organic molecule.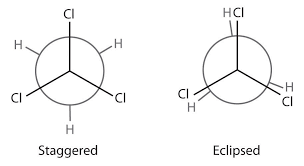
Furthermore, a
180^@ dihedral angle does not really tell you what the bond angles are of the"X"-"C"-"C"-"Y" bond, where"X" is the atom at the top middle of a Newman projection and"Y" is the atom at the bottom middle of the same Newman projection. -
Answer:
A sawhorse projection is a view of a molecule down a particular carbon-carbon bond.
Explanation:
Groups connected to both the front and back carbons are drawn using sticks at 120° angles.
A sawhorse projection is similar to a Newman projection, but it shows the carbon-carbon bond that is hidden in a Newman projection.
Just as with Newman projections, you can draw sawhorse projections in eclipsed and staggered conformations.
Below is a sawhorse projection of the gauche conformation of butane.
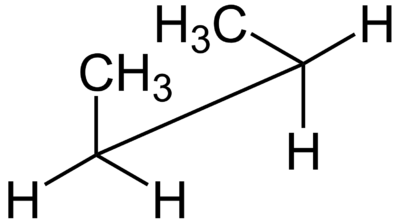
They are called sawhorse projections because the eclipsed conformation looks like a carpenter's sawhorse.

Sawhorse projections are useful for determining if two molecules are enantiomers or diastereomers.
They make it easier to see if the structures are mirror images or superimposable.
Here are the sawhorse and Newman projections of butan-2-ol.
