The Product and Quotient Theorems
Key Questions
-
Well, I can think of an application when studying circuits in AC. I am not sure if you know about circuits in Alternate Current but the fact that the current continuously changes can cause difficulties in analyzing the performance of the entire circuit or of some of the elements of it. For this reason is better to use complex numbers to represent the response of the various devices in your circuit to avoid dealing with trig. functions that, as you may know, are quite difficult to manipulate. So, basically, the person that deals with AC "likes" to use complex numbers and their representation in polar form to "simplify" the operations and the maths.
As an example you can have the following circuit where you want to find the current and its phase:
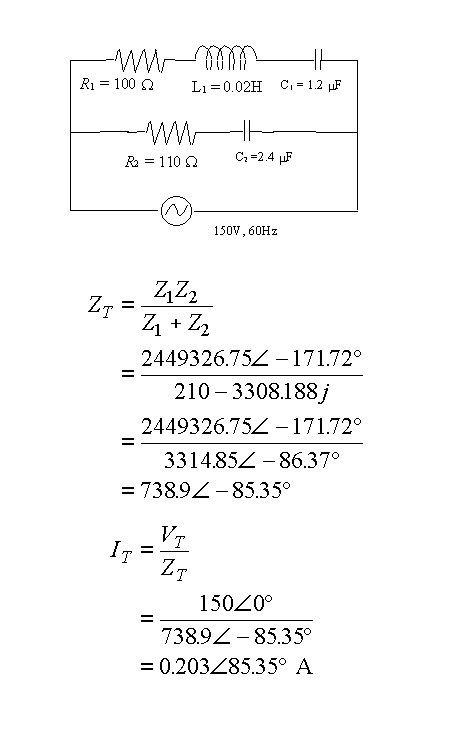
As you can see you can get an equivalent impedance#Z_T# which is a parallel of the upper#Z_1# (R+L+C)and lower#Z_2# (R+C) impedance (correspondent, say, to our#R_(eq)# in a normal DC circuit) but do not worry about the derivation of it, the important thing is that it is in complex polar form!
And then you use it into an AC form of Ohm's Law to find#I_T# !!!!Hope it helps!
-
Given two complex numbers in polar coordinates by their modulo
#r# and polar angle#phi# :
#z_1=r_1*(cos phi_1+i*sin phi_1)# and
#z_2=r_2*(cos phi_2+i*sin phi_2)# where#r_2 != 0# ,Then the result of the division of the first by the second is equal to
#z_1/z_2=(r_1/r_2)*[cos (phi_1-phi_2)+i*sin (phi_1-phi_2)]#
This is the quotient theorem.The trigonometric proof of this theorem is easier to start with a product theorem:
#z_1*z_2=(r_1*r_2)[cos (phi_1+phi_2)+i*sin (phi_1+phi_2)]# The proof:
#r_1(cos phi_1+i*sin phi_1) * r_2(cos phi_2+i*sin phi_2) =#
#= r_1*r_2*(cos phi_1*cos phi_2 + i^2*sin phi_1*sin phi_2 + i*sin phi_1*cos phi_2 + i*cos phi_1*sin phi_2) =#
#= r_1*r_2*[(cos phi_1*cos phi_2 - sin phi_1*sin phi_2) + i*(sin phi_1*cos phi_2 + cos phi_1*sin phi_2)] =#
#=r_1*r_2*[cos(phi_1+phi_2)+i*sin(phi_1+phi_2)]# Verbally, the product theorem states that, to multiply two complex numbers defined in polar form via modulo and a polar angle, modulo of one complex number is multiplied by another and the angles are added together.
For complex numbers with modulo
#1# , geometrically, multiplication is a rotation of a vector representing the first complex number counterclockwise by the angle of the second number.Back to the division of complex numbers in polar form.
To prove the quotation theorem mentioned above, all we have to prove is that#z_1/z_2# in the form we presented, multiplied by#z_2# , produces#z_1# .Indeed, using the product theorem,
#(z_1/z_2)*z_2 = {(r_1/r_2)[cos (phi_1-phi_2)+i*sin (phi_1-phi_2)]}*r_2(cos phi_2+i*sin phi_2)=#
#=(r_1/r_2)*r_2*[cos(phi_1-phi_2+phi_2)+i*sin (phi_1-phi_2+phi_2)]=#
#= r_1*(cos phi_1+i*sin phi_1)# End of proof.
Verbally, the quotient theorem states that, to divide one complex number by another, modulo of the first complex number is divided by another and the angle of the second one is subtracted from the first.
Geometrically, on the unit circle, it represents a clockwise rotation of the first vector by an angle of the second.
-
Answer:
#zw = (r_1 *r_2)(cos(theta_1 +theta_2) + isin(theta_1 +theta_2))# Explanation:
Alright, so the polar form of a complex number
#z=a+bi# is#z= r(cos(theta) + isin(theta))# Suppose you have a complex number
#w# which you wanted to multiply by#z# , then this will be the rule you need to use#zw = (r_1 *r_2)(cos(theta_1 +theta_2) + isin(theta_1 +theta_2))#