What is the length of the hypotenuse of a right triangle if the two other sides are of lengths 8 and 1?

Question

2258 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-14T00:54:14

$\sqrt{65}$ $sqrt(65)$

In the picture below, the Pythagorean Theorem tells us that:

$a^{2} + b^{2} = c^{2}$ $a^2+b^2=c^2$

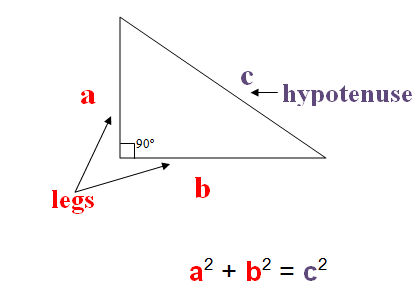
![http://www.algebra-class.com/http://pythagorean-theorem.html](https://useruploads.socratic.org/pq5TPYPSoa2h8zhrbXqS_pythagoras1.gif)

If we apply this theorem to the given question, then:

$a = 8$ $a=8$

$b = 1$ $b=1$

$c = ?$ $c=?$

Using the Pythagorean Theorem, start by rearranging the equation in terms of $c$ $c$ . Then substitute your known values into the equation.

$a^{2} + b^{2} = c^{2}$ $a^2+b^2=c^2$

$c = \sqrt{a^{2} + b^{2}}$ $c=sqrt(a^2+b^2)$

$c = \sqrt{8^{2} + 1^{2}}$ $c=sqrt(8^2+1^2)$

Solve.

$c = \sqrt{64 + 1}$ $c=sqrt(64+1)$

$color(green)(|bar(ul(color(white)(a/a)c=sqrt(65)color(white)(a/a)|)))$

$:.$ , the length of the hypotenuse is $sqrt(65)$ .