How do you find the vertex and the intercepts for #y = (x − 3)(4x + 2) #?
1 Answer
You must first write the function in standard form, by distributing, and then complete the square into vertex form.
Explanation:
Before we do what was mentioned above, we can determine the y intercept, as well as the x intercepts.
There will therefore be x intercepts at
The y intercept is at
Now for the vertex:
Completing the square is a process for converting quadratic functions from standard form (
In vertex form,
Here is the graph of this function:
graph{y = (x - 3)(4x + 2) [-40, 40, -20, 20]}
Practice exercises:
- Determine the vertex and intercepts of the following functions:
a)
b)
- Use the following graph of
#y = f(x)# to answer questions a), b), c) and d)
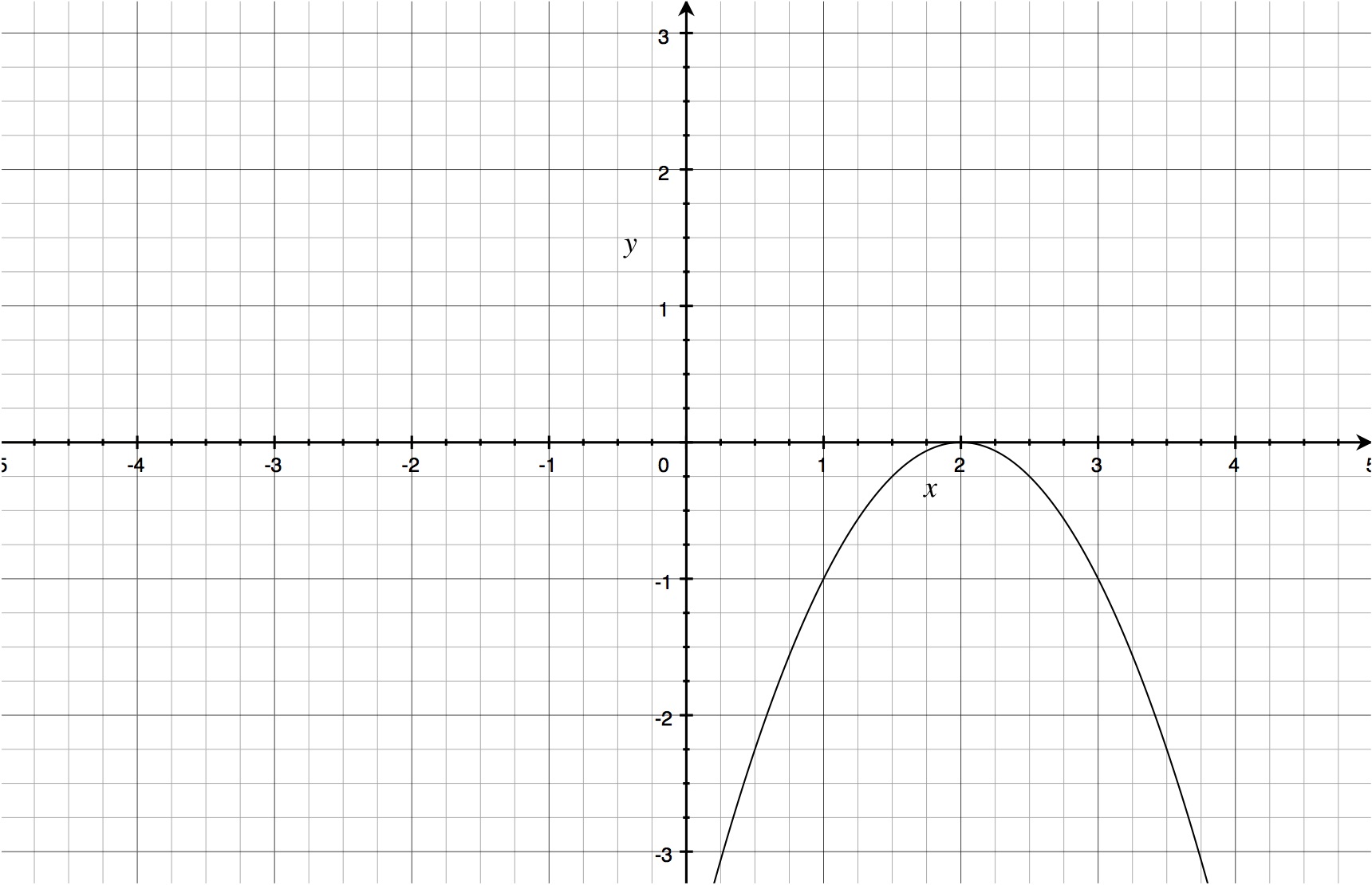
a) What is the vertex of this function?
b) What are the x intercepts of this function?
c) Challenging!! What is this graph's equation?
d) Challenging!! Use the equation of the graph to find the coordinates of the y intercept.
Hopefully this helps!

