Question

How do you find the parametric equations for the rectangular equation `x^2+y^2=16`?

Answer 1

`((x), (y)) = ((4 cos t),(4 sin t))`

Explanation:

the most sensible/common paramaterisation here is to recognise that this is a circle, or just to acknowledge the Pythagorean identity: `cos^2 t + sin^2 t = 1`, that we could use here

so if we take your equation

`x^2+y^2=16`

...and re-write it slightly as

`(x/4)^2+(y/4)^2=1`

then we see that if we set

`x/4 = cos t` and `y/4= sin t`

we can use the identity

So the parameterisation is

`((x), (y)) = ((4 cos t),(4 sin t))`

so that, just to check, `x^2+y^2= 4^2 cos^2 t + 4^2 sin^2 t = 16`

Answer 2

`{x = 4(1-m^2)/(1+m^2), y = (8m)/(1+m^2)}` for `-oo < m < oo`

Explanation:

This circle

`c->x^2+y^2=4^2`

is origin centered with radius `4`. Think of a line with a fixed point in `p_0={-4,0}`.

This line intersects the circle in one more point, depending on its declivity.

`l -> y - y_0 = m(x-x_0)` or
`l->y = m(x+4)`

The intersection `c nn l` is obtained solving

#{ (y-m(x+4)=0), (x^2+y^2-4^2=0) :}#

giving for `{x,y}` the solutions

`{x = -4,y=0}` the fixed point, and
`{x = 4(1-m^2)/(1+m^2), y = (8m)/(1+m^2)}`

This last solution, gives us a circle's parameterization for `-oo < m < oo`

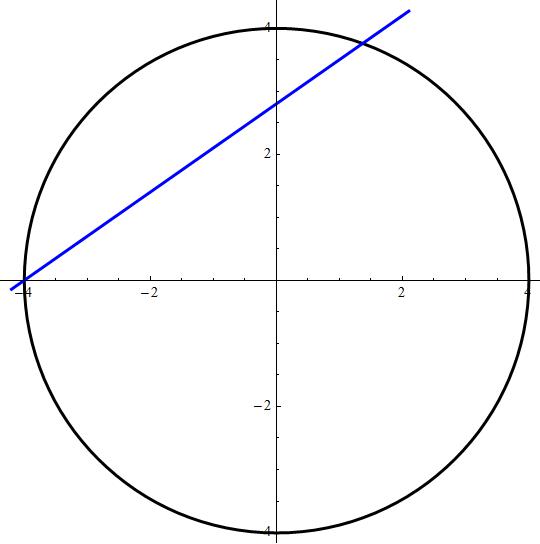
Attached also a comparative plot for `x(m)` in blue and for `y(m)` in red. As can be observed, for `-1 le m le 1` the parameterization covers the positive `x` values and the whole `y` range. To obtain the negative `x` values we need to extend the range until `pm oo`