The line can be re-written as follows
#vec l = ((1+t),(3-t),(2t)) = ((1),(3),(0)) + t ((1),(-1),(2))#
#= ((1),(3),(0)) + t' 1/sqrt(6) ((1),(-1),(2))#
#=vec (OQ) + t' hat u#
where
#Q = ((1),(3),(0))# is a point on the line
and
#hat u = 1/sqrt(6) ((1),(-1),(2)) # is the unit vector along its direction.
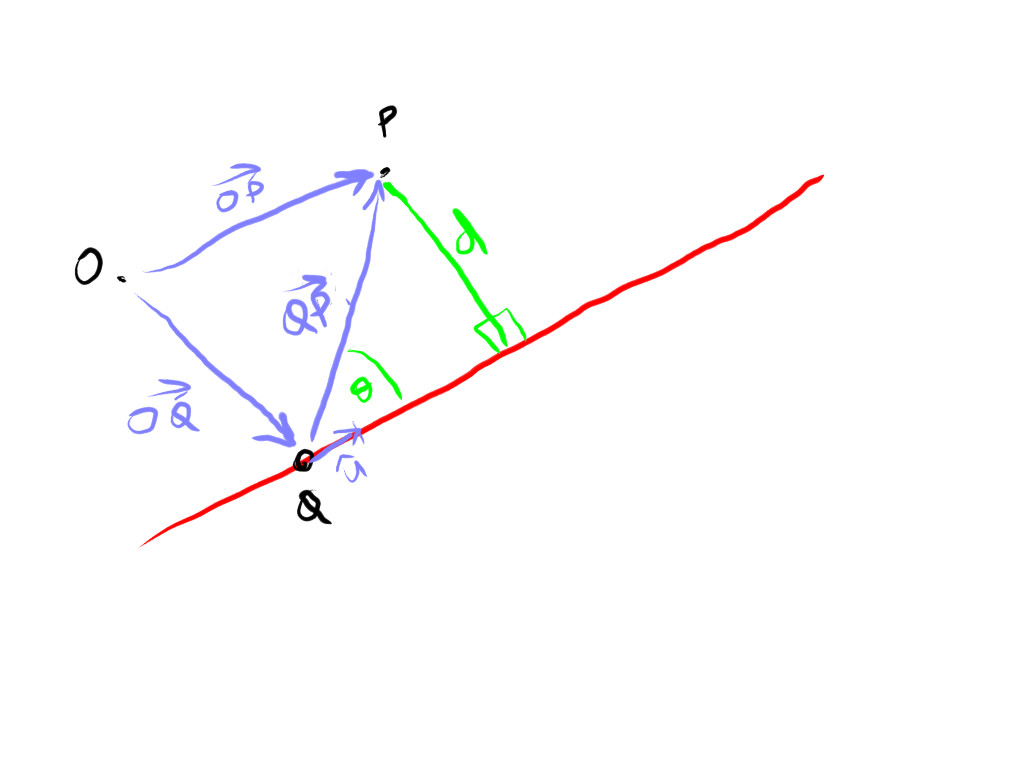
From the sketch, the shortest distance, #d#, between point P and line, is a straight line that runs orthogonal to the line. Distance d is given by
#d = abs(vec(QP)) sin theta = abs (vec(QP) times hat u)#
(NB # abs (vec(QP) times hat u )=abs( abs(vec(QP)) abs ( hat u) sin theta )# but #abs( hat u) = 1#)
#vec(QP) = vec(OP) - vec (OQ)#
#= ((1),(1),(5)) - ((1),(3),(0)) = ((0),(-2),(5)) #
# vec(QP) times hat u = 1/sqrt(6) det ((hat i, hat j, hat k),(0,-2,5),(1,-1,2))#
#=1/sqrt(6)( hat i + 5 hat j + 2 hat k) = vec n#
The vector cross product is also vector, #vec n#, which is perpendicular to both #vec (QP)# and #hat u#. We can check this first by evaluating the scalar dot products to zero:
#hat u * vec n =1/sqrt(6) (1,-1,2)*(1,5,2) = 0#!!
#vec(QP) * vec n = (0,-2,5)*(1,5,2) = 0#!!
So finally,
#abs (vec(QP) times hat u) = abs(vec n)#
#= abs (1/sqrt(6)( hat i + 5 hat j + 2 hat k)) #
#= 1/sqrt(6) * sqrt( 1^2 + 5^2 + 2^2)#
#= sqrt(5) #


