Question

Given the equilateral triangle inscribed in a square of side `s` find the ratio of `Delta BCR " to " DeltaPRD`?

Answer 1

`(DeltaBCR)/(DeltaPRD)=1/2`

Explanation:

Considering the figure to be symmetric w.r.t. `BD`, `/_CBR=(90^o-60^o)/2=15^o`

and side `CR` of `DeltaBPR` is given by

`CR=sxxtan15^o=(sqrt3-1)/(sqrt3+1)s`, where `BC=s`.

Area of `DeltaBCR=(BCxxCR)/2=sxx(sqrt3-1)/(sqrt3+1)s/2=(sqrt3-1)/(sqrt3+1)s^2/2`

Area of `DeltaPRD=(DR^2)/2=((s-CR)^2)/2=(s-(sqrt3-1)/(sqrt3+1)s)^2/2`

`(1-(sqrt3-1)/(sqrt3+1))^2s^2/2=((sqrt3+1-sqrt3+1)/(sqrt3+1))^2s^2/2=4/(sqrt3+1)^2s^2/2`

Hence `(DeltaBCR)/(DeltaPRD)=((sqrt3-1)/(sqrt3+1)s^2/2)/(4/(sqrt3+1)^2s^2/2)=((sqrt3-1)/(sqrt3+1))/(4/(sqrt3+1)^2)=((sqrt3-1)(sqrt3+1)^2)/(4(sqrt3+1))`

= `((sqrt3-1)(sqrt3+1))/4=(3-1)/4=2/4=1/2`

Answer 2

`(DeltaBCR)/(DeltaPRD)=1/2`

Explanation:

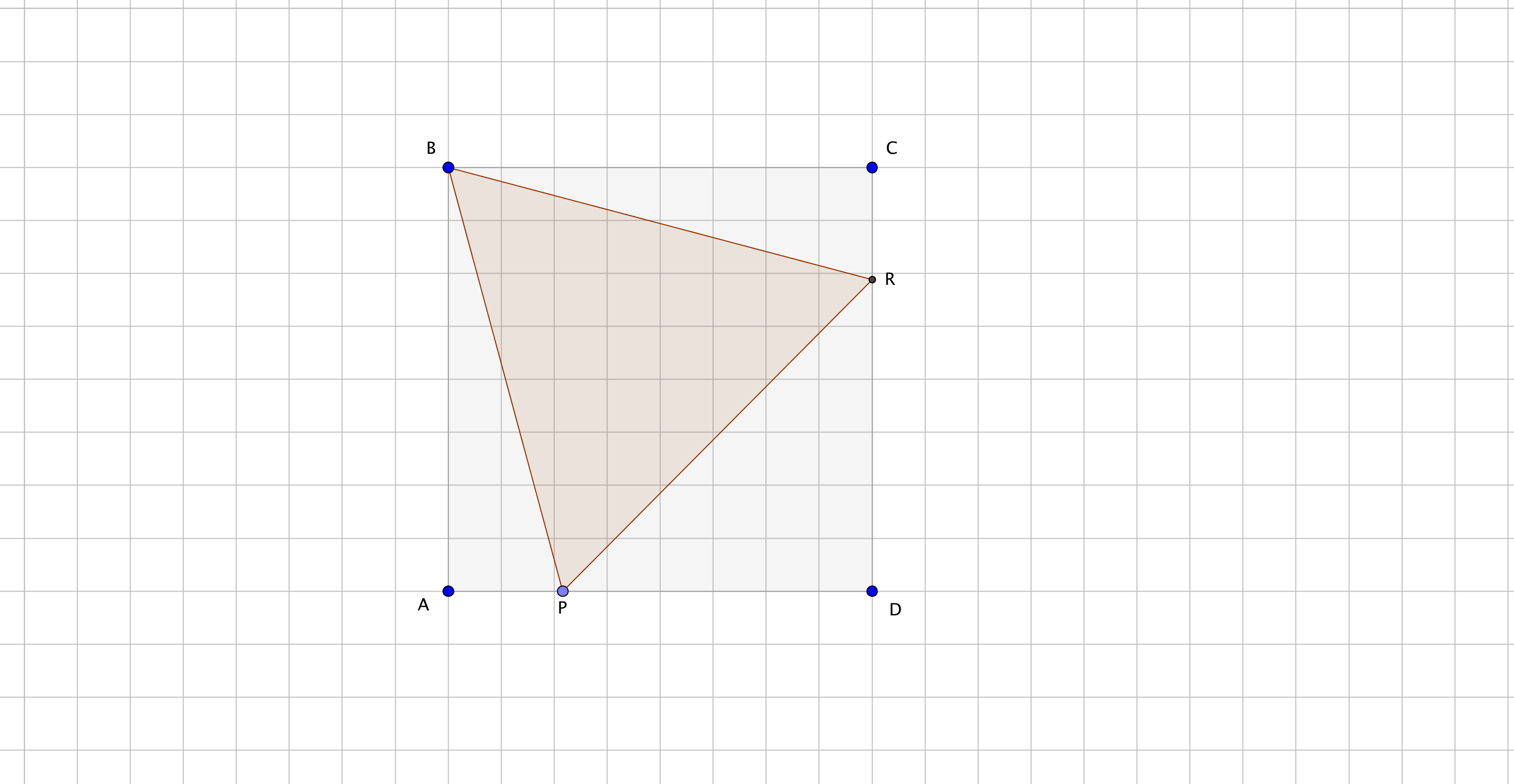
As per given figure `DeltaBCR ~=DeltaABP`
Since `/_BCR=/_ABP=90^@->"angle of a square"`

`"hypotenuse "BR ="hypotenuse "BP`
( sides of equilateral `DeltaBRP`)

`AB=BC->"sides of square ABCD"`

So `/_CBR=/_ABP`

Using trigonometry

In triangle BCR
`/_CBR=/_ABP=1/2(/_ABC-/_PBR)`

`=(90^@-60^@)/2=15^@`

and `/_BRC=90^@-15^@=75^@`

If the length of each side of the equilareral triangle BPR be a,then
`BC=asin/_CBR=acos15^@`

`CR=asin/_CBR=asin15^@`

For `DeltaPRD`

`/_PRD=(180-/_BRC-/_BRP)`

`=180^@-75^@-45^@=45^@`

So `PD=DR=PRcos45^@=acos45^@=asin45^@`

Now

`(DeltaBCR)/(DeltaPRD)`

`=(cancel(1/2)xxCRxxBC)/(cancel(1/2)xxPDxxDR)`

`=(asin15^@xxcos15^@)/(acos45^@xxasin45^@)`

`=(2cos15^@xxsin15^@)/(2cos45^@xxsin45^@)`

`=sin30^@/sin90^@`

`=sin30^@=1/2`

Without using trigonometry

We have shown above `DeltaBCR ~=DeltaABP`

So CR=AP

Now

`DR=CD-CR=AD-AP=DP`

Applying Pythagoras theorem for `DeltaPRD` we get

`PR^2=DP^2+DR^2=2DR^2`

`=>BR^2=2DR^2->"since "PR=BR`

Niw applying Pythagoras theorem for `DeltaBRC` we get

`BR^2=BC^2+CR^2`

So `2DR^2=BC^2+CR^2`

`=>2DR^2=BC^2+CR^2`

`=>2DR^2=CD^2+CR^2`

`=>2DR^2=(CR+DR)^2+CR^2`

`=>2DR^2=CR^2+DR^2+2CR*DR+CR^2`

`=>2DR^2-DR^2=2CR^2+2CR*DR`

`=>DR^2=2CR^2+2CR*DR`

`=>1/2*DR^2=CR^2+CR*DR`

`=>1/2*DR^2=CR(CR+DR)`

`=>1/2*DR*PD=2*1/2*CR*CD`

`=>1/2*DR*PD=2*1/2*CR*BC`

`=>DeltaPRD=2*DeltaBCR`

`=>(DeltaBCR)/(DeltaPRD)=1/2`