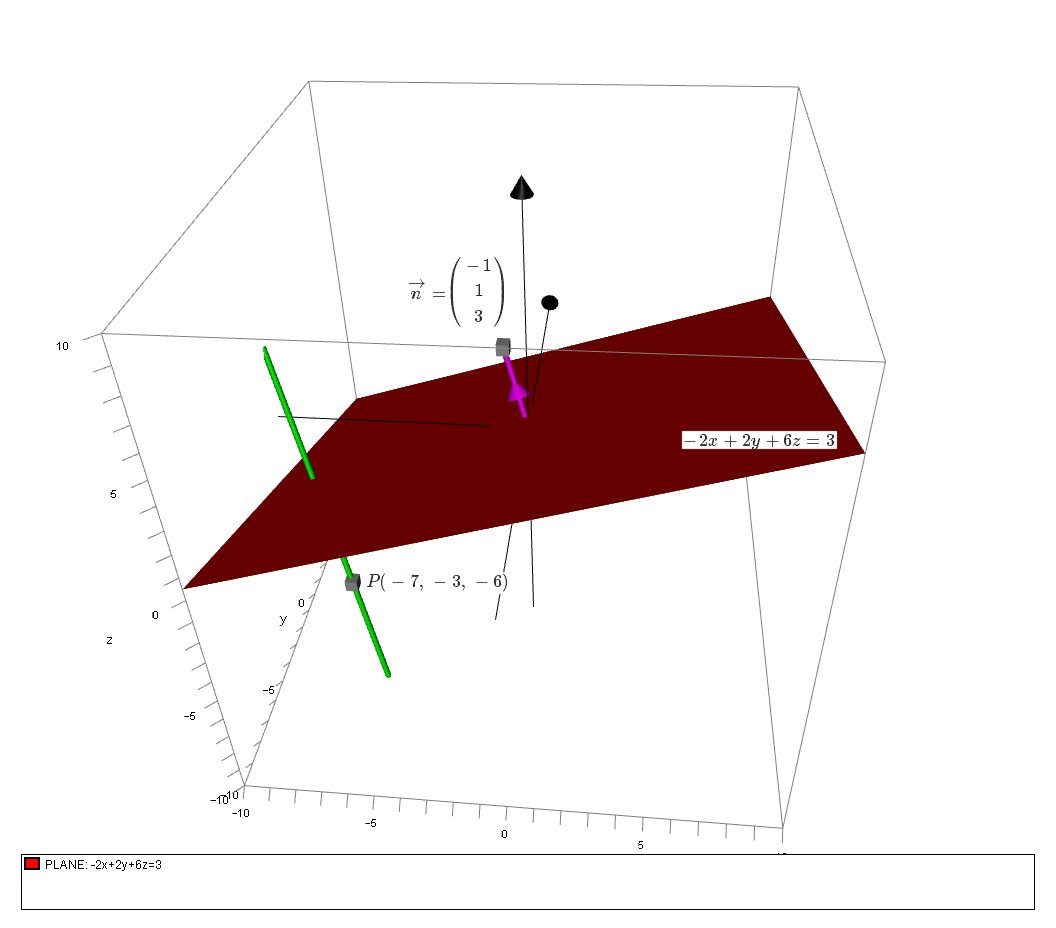
How do you find parametric equation for the line through the point P(-7,-3,-6) and perpendicular to the plane -2x + 2y + 6z =3?
1 Answer
We can write the parametric equations as;
# {: (x=-7-lamda), (y=-3+lamda), (z=-6+3 lamda) :} #
Explanation:
If we examine the plane equation
# vec (n) = ( (-2), (2), (6) ) = 2( (-1), (1), (3) )#
So then the vector equation of the line that has this direction and passes through
# vec(r)=( (-7), (-3), (-6) ) + lamda ( (-1), (1), (3) ) #
So we can write the generic coordinates for any point on the lines as:
# ( (x), (y), (z) ) = ( (-7), (-3), (-6) ) + lamda ( (-1), (1), (3) ) = ( (-7-lamda), (-3+lamda), (-6+3lamda) )#
So we can write the parametric equations as;
# {: (x=-7-lamda), (y=-3+lamda), (z=-6+3 lamda) :} #
We can verify this with a 3D graph: