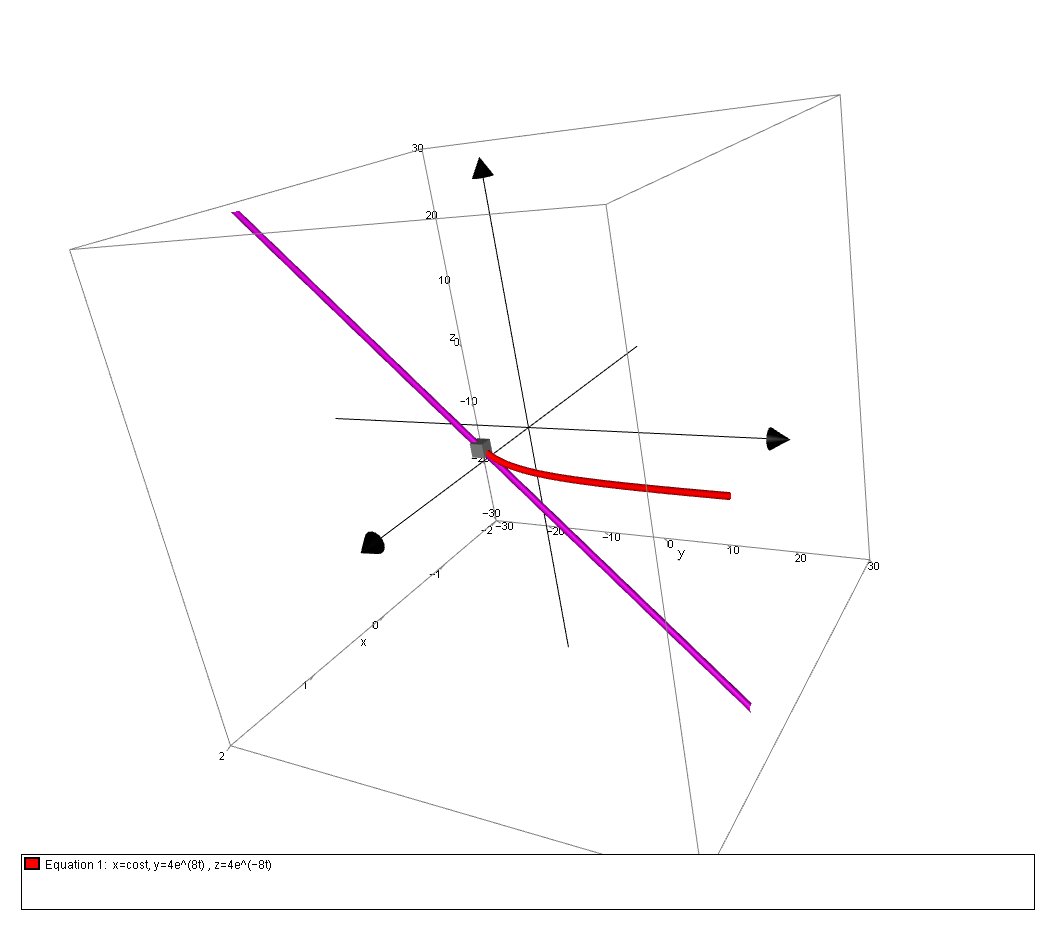
How do you find parametric equations for the tangent line to the curve with the given parametric equations at the point #( 1, 4, 4)#. #x = cos(t), y = 4e^8t, z = 4e^ -8t#?

Question

4492 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-14T23:13:25

# x=1 #
# y=4+lamda #
# z=4-lamda #

We have parametric equations as functions of #t# for #x#, #y# and #z# so we can form the derivatives wrt t for each variable:

# x=cost \ => dx/dt=-sint #
# y=4e^(8t) \ \ => dy/dt = 32e^(8t) #
# z = 4e^(-8t) => dz/dt = -32e^(8t) #

In order to find the normal at any particular point in vector space we use the Del, or gradient operator:

# grad f(t) = dx/dt hat(i) + dy/dt hat(j) + dz/dt hat(k)#
# \ \ \ \ \ \ \ \ \ \ = -sint hat(i) + 32e^(8t) hat(j) - 32e^(-8t) hat(k) #

So for the particular point #(1, 4,4)# we need to establish the corresponding value of #t#, which by inspection is #t=0#.

So for this particular point, the normal vector to the surface is given by:

# grad f(0) = 0 hat(i) + 32 hat(j) - 32 hat(k) #
# " " = 32 hat(j) - 32 hat(k) #
# " " = 32 (hat(j) - hat(k)) #

So the tangent line is a line with direction #hat(j) - hat(k)# that passes through the point #(1, 4,4)#, which therefore has the vector equation:

# vec r = ( (1), (4), (4) ) + lamda ( (0), (1), (-1) ) #

Which we can therefore parametrise (using #lamda#) as follows

# x=1 #
# y=4+lamda #
# z=4-lamda #

We can confirm this graphically: Here is the surface (red)with the tangent line (purple):
enter image source here