A triangle has two corners with angles of # ( pi ) / 2 # and # ( pi )/ 6 #. If one side of the triangle has a length of #5 #, what is the largest possible area of the triangle?

Question

1269 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-27T07:45:09

The largest possible area is #21.65#.

As the two angles are #pi/2# and #pi/6#, the third angle is

#pi-pi/2-pi/6=(6pi)/6-(3pi)/6-pi/6=(6pi-3pi-pi)/6=(2pi)/6=pi/3#

As the smallest angle of the three is #pi/6#,

area will be largest if side with length #5# is opposite the smallest angle #pi/6#

Such a triangle is typical #30^@-60^@-90^@# triangle and looks like as shown below

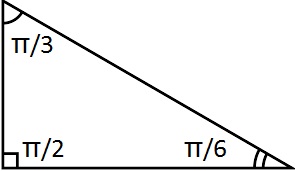
enter image source here

In such a right angled triangle, if smallest side is #5#, hypotenuse is #5xx2=10# and third side #5xxsqrt3#.

As the two sides forming the right angle in right angled triangle are #5# and #5sqrt3#, the area of triangle is

#1/2xx5xx5sqrt3=25/2xx1.732=21.65# and

The largest possible area is #21.65#.