Question

Al-Khwarizmi, the father of modern mathematics try to solve the following: One square and ten roots of the same are equal to thirty-nine dirhems - What must be the square that when increased by ten of its own roots, amounts to thirty-nine?

Answer 1

Answer is `3`

Explanation:

As the problem states that

"what must be the square that when increased by ten of its own roots, amounts to thirty-nine"

it means if the number is `x`, then

`x^2+10x=39` - and adding `25` on both sides we get

`x^2+10x+25=39+25`

or `x^2+10x+25=64`

or `(x+5)^2-64=0`

i.e. `(x+5+8)(x+5-8)=0`

i.e. `(x+13)(x-3)=0`

Hence, either `x=3` or `x=-13`

It may, however, be noted that in the times of Al-Khwarizmi, negative numbers were not considered and further, the problem emanates from the geometric problem represented by following figure (not drawn to scale - it is in fact a square),

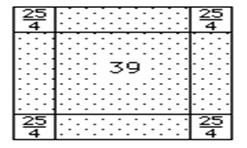
where Al-Khwarizmi sought solution to the side of inner square, where shaded area that forms the box is `39` units. The inner square is `x^2` and four rectangles are `4×5/2×x=10x`.

As it was essentially a geometric figure, `-13` was ruled out.