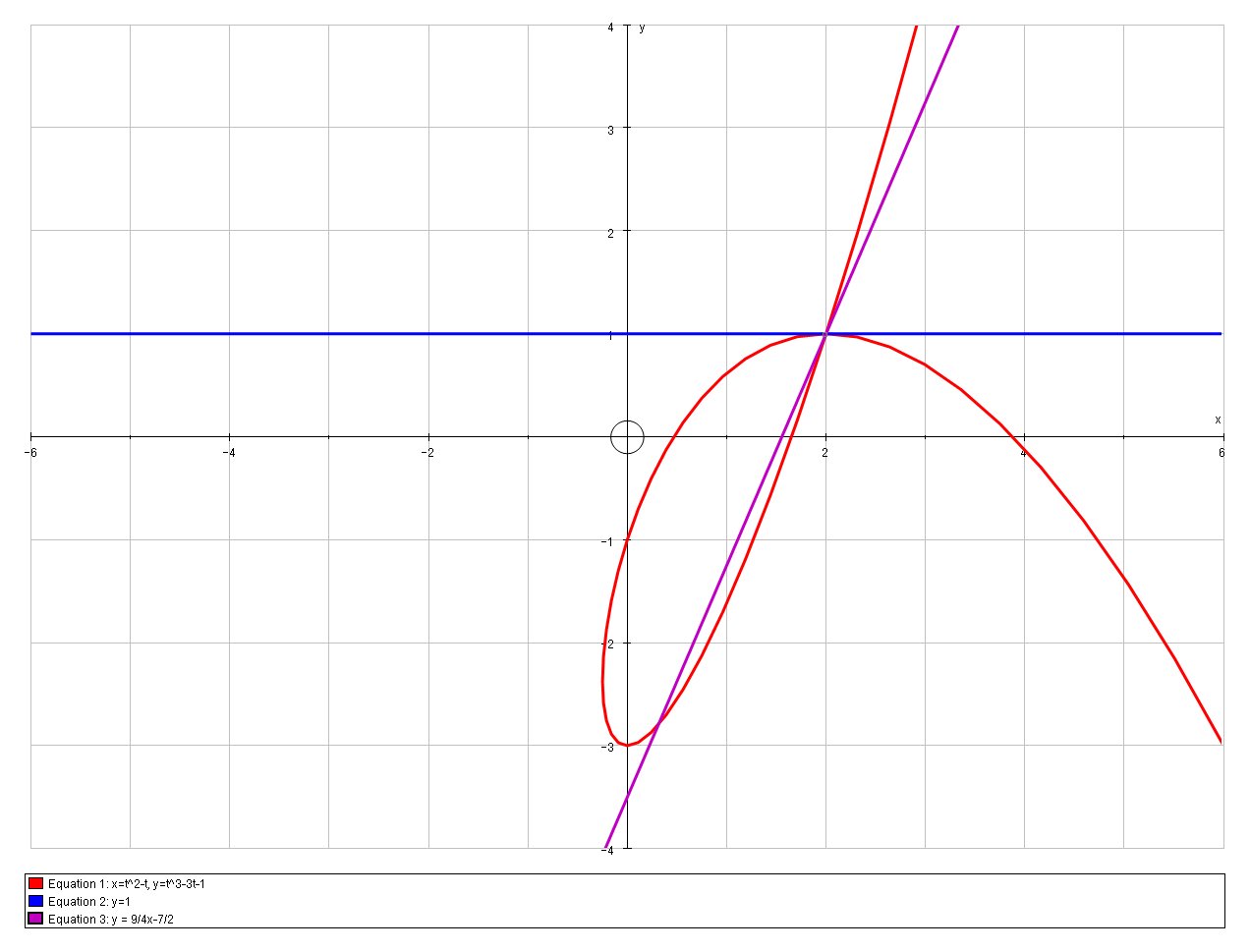
How do you find the equations of tangent lines at the point where the curve crosses itself #x=t^2-t# and #y=t^3-3t-1#?
1 Answer
# y=1 #
and
# y = 9/4x-7/2 #
Explanation:
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is
We have:
# x = t^2-t #
# y = t^3-3t-1 #
Firstly, let us find the coordinates where the curve crosses itself. In which case there will be an ordered pair
# \ \ \ \ \ \ \ \ \ alpha^2-alpha = beta^2-beta# ..... [1]
# alpha^3-3alpha-1 = beta^3-3beta-1# ..... [2]
From [1] we have:
# alpha^2-beta^2 =alpha -beta #
# :. (alpha+beta)(alpha-beta)=alpha -beta #
# :. alpha+beta= 1 #
# :. beta =1-alpha#
From [2] we have:
# alpha^3-beta^3 =3alpha -3beta#
# :. (alpha - beta)(alpha^2 + alpha beta + beta^2) = 3(alpha -beta)#
# :. alpha^2 + alpha beta + beta^2 = 3#
# :. alpha^2 + alpha (1-alpha) + (1-alpha)^2 = 3#
# :. alpha^2 + alpha -alpha^2 + 1-2alpha+alpha^2 = 3#
# :. alpha^2-alpha-2 = 0#
# :. (alpha+1)(alpha-2) = 0#
# :. alpha=-1,2#
And with these values of
# t=-1 => x=2,y=1 #
# t=\ \ \ \ \ 2 => x=2,y=1 #
Thus the curve touches itself when
Then differentiating implicitly wrt
# dx/(dt) = 2t # and# dy/(dt) = 3t^2-3 #
# dy/dx = (dy//dt)/(dx//dt) = (3t^2-3)/(2t) #
So at the parametric coordinate
# m_1 = dy/dx = (3-3)/(2) = 0#
So the tangent passes through
# y - 1 = 0 #
# :. y = 1 #
And, at the parametric coordinate
# m_2 = dy/dx = (12-3)/(4) = 9/4#
So the tangent passes through
# y - 1 = 9/4(x-2) #
# :. y - 1 = 9/4x-9/2 #
# :. y = 9/4x-7/2 #