Question

Why is `"Ni"("CN")_4^(2-)` diamagnetic but `"NiCl"_4^(2-)` paramagnetic?

Answer 1

Well is not one square planar, and the other tetrahedral.........??

Explanation:

`""^(-)C-=N` is the classic low spin ligand. Its dagger like shape allows its close approach to the metal centre, and STRONG discrimination between the axial and the non-axial `"d-orbitals"` in terms of energy.

All of this will be explained much better in your inorganic text; and it will probably give detailed descriptions of splitting diagrams.......

Answer 2

This is due to the former complex being square planar and the latter being tetrahedral. Examine their crystal field splitting diagrams at the bottom of the answer and the supplementary explanation to see where the two unpaired electrons in `["NiCl"_4]^(2-)` come from.

---

DISCLAIMER: LONG ANSWER!

TENDENCIES OF `bb(d^8)` METALS

`"Ni"^(2+)`, a `d^8` metal cation, is the metal center here, and `bb(d^8)` metals tend to make four-coordinate complexes like these, which are either tetrahedral or square planar.

The difference in energy between these configurations tends to be small. Tetrahedral `d^8` tends to be high spin, while square planar `d^8` tends to be low-spin.

REGARDING LIGAND FIELD STRENGTHS

Consider the following diagram for octahedral complexes, which shows the difference in (ligand) field splitting energies for `pi` acceptors, `sigma` donors, and `pi` donors from left to right:


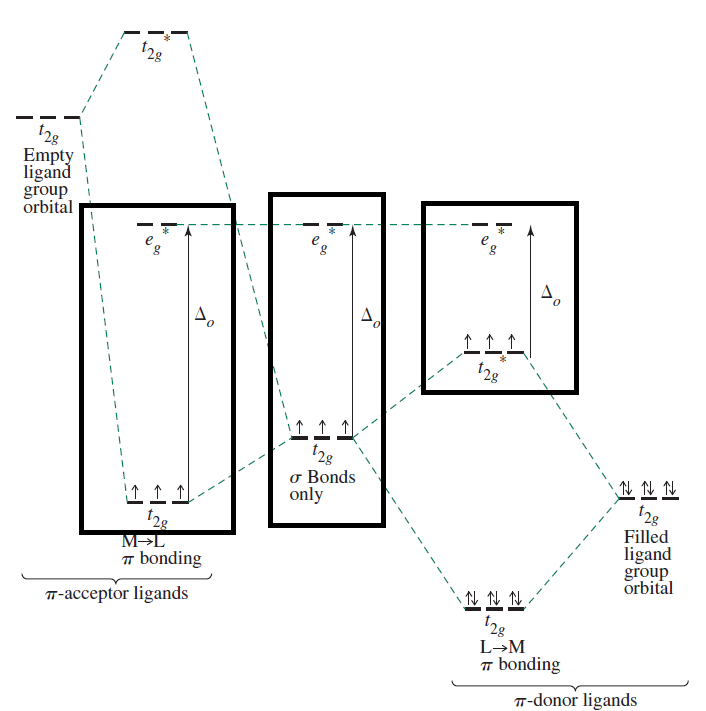
Basically, `pi` donors destabilize the `t_(2g)` orbitals, `sigma` donors destabilize the `e_g^"*"` orbitals, and `pi` acceptors stabilize the `t_(2g)` orbitals.

In the spectrochemical series, `"Cl"^(-)` is a weak-field ligand as it is a `pi` donor, while `"CN"^(-)` is a strong-field ligand as it is a `pi` acceptor AND `sigma` donor.

This further means that...

• `"Cl"^(-)`, a weak-field, `pi` donor ligand, promotes high-spin complexes, since electron-pair repulsions are minimized, giving minimal crystal field energy splitting, and Hund's rule applies for such nearly degenerate `d` orbitals (fill orbitals with one electron at a time, then double up).

• `"CN"^(-)`, a strong-field, `pi` acceptor AND `sigma` donor ligand, promotes low-spin complexes, since electron-pair repulsions are maximized and the crystal field splitting energy increases significantly. How you fill orbitals for low-spin complexes is to follow Hund's rule for that energy level, allowing electron pairing, then go to the next energy level.

Hence, the chloride complex would favor tetrahedral, and the cyanide complex would favor square planar.

CRYSTAL FIELD SPLITTING DIAGRAMS

Their blank `d`-splitting diagrams within the realm of crystal field theory are:

`["Ni"("CN")_4]^(2-)`:

![https://upload.wikimedia.org/]()

The `d` orbitals fill with `8` electrons, then, with a low spin configuration. You can see that an even number of `d` orbitals will get filled (`d_(yz),d_(xz),d_(z^2),d_(xy)`) with an even number of `3d` electrons.

This gives rise to a diamagnetic configuration, as expected.

`["Ni""Cl"_4]^(2-)`:

![http://scienceworld.wolfram.com/]()

The `d` orbitals here fill with `8` electrons, but instead, high spin. So, the `d_(z^2)` and `d_(x^2 - y^2)` fill with one electron each, then the `d_(xy)`, `d_(xz)`, and `d_(yz)` with one electron each, and then pairing occurs only after that, filling the `d_(z^2)`, `d_(x^2-y^2)`, and `d_(xy)` completely.

This leaves two unpaired electrons in the `t_2` orbitals, and thus this complex is paramagnetic with two unpaired electrons, as expected.