Question

What is the area bounded by the parametric equations? : `x=acos theta` and `y=bsin theta`

Answer 1

It is vital when dealing with parametric equations (or polar coordinates) to get a full understanding of the effect of the parameter on the curve (and sign) so that positive and negative areas can be determined and dealt with.

We have parametric equations:

`x=acos theta`
`y=bsin theta`

Where `a,b gt 0`. Let us first look at how `x=acos theta` and `y=bsin theta` behave over the given domain `0 le theta le 2pi`

`0 le theta le pi/2 => x>0, y>0`
`pi/2 le theta le pi => x<0, y>0`
`pi le theta le (3pi)/2 => x<0, y<0`
`(3pi)/2 le theta le 2pi => x>0, y<0`

So we can see that as `theta` varies on the domain we move uniformly from Q1, Q2, Q3 then Q4. Thus `0 le theta le pi` (Q1,Q2) will contribute positively and `pi le theta le 2pi` (Q3,Q4) will contribute negatively.

If we now examine the parametric curve

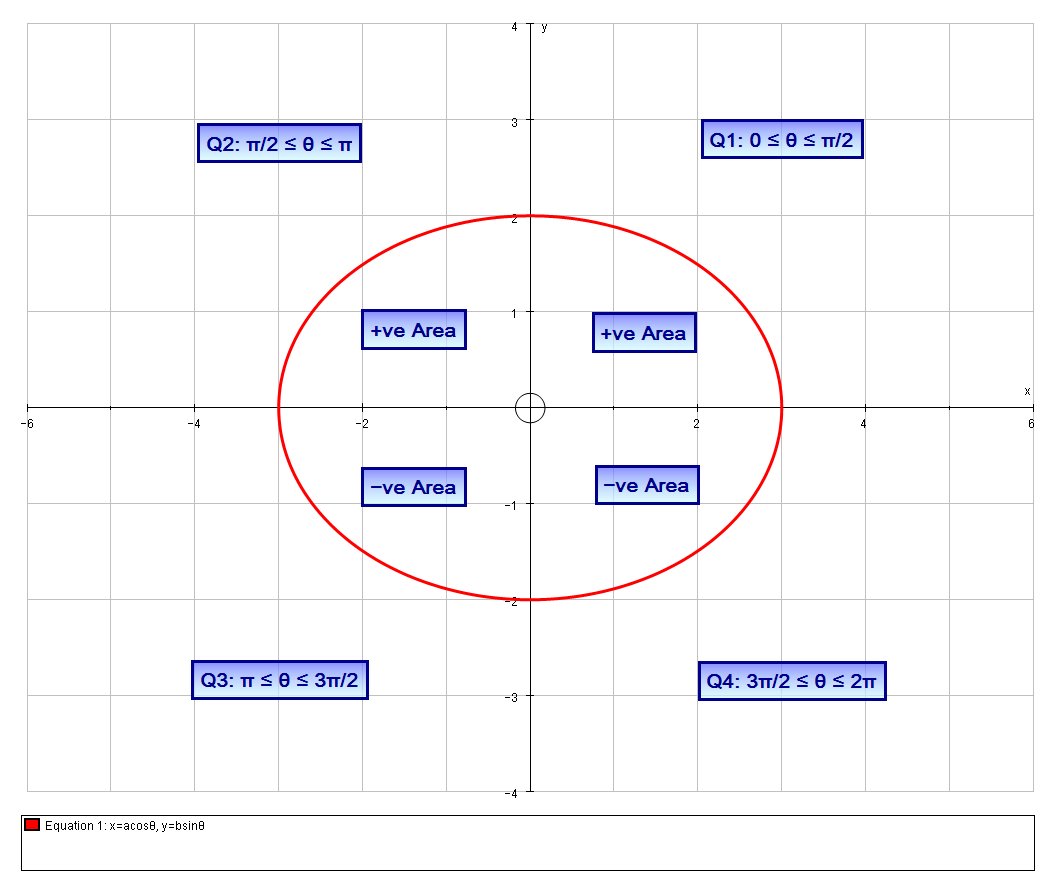
We can see that we can evaluate the area by symmetry as `4` times that of Q1

Thus we can represent the area of the ellipse by:

`A = 4 \ int_(x=0)^(x=a) \ y \ dx`

Now we will change variable from `x` to `theta` to actually perform the integration:

`x=acos theta => dx/(d theta)=-asin theta`
`y=bsin theta`

And for the limits of integration we have:

`x=0 => acos theta =0 => theta=pi/2`
`x=a => acos theta =a => theta=0`

And so we can evaluate the integral as follows;

`A = 4 \ int_(pi/2)^(0) \ (bsin theta)(-asin theta) \ d theta`
`\ \ = -4ab \ int_(pi/2)^(0) \ sin^2 theta \ d theta`
`\ \ = 4ab \ int_(0)^(pi/2) \ sin^2 theta \ d theta`
`\ \ = 4ab \ int_(0)^(pi/2) \ sin^2 theta \ d theta`
`\ \ = 4ab \ int_(0)^(pi/2) \ (1-cos2theta)/2 \ d theta`
`\ \ = 2ab \ int_(0)^(pi/2) \ 1-cos2theta \ d theta`
`\ \ = 2ab \ [theta-(sin2theta)/2]_(0)^(pi/2)`

`\ \ = 2ab \ {(pi/2-0)-(0-0)}`

`\ \ = pi ab`