Question

A triangle has sides A,B, and C. If the angle between sides A and B is `(7pi)/8`, the angle between sides B and C is `pi/12`, and the length of B is 12, what is the area of the triangle?

Answer 1

`color(green)("Area of " Delta " " A_t = 54.62 " sq units"`

Explanation:

`hat A = pi/12, hat C = (7pi)/8, b = 12, " To find the area of " Delta`

`hat B = pi - hat A - hat C = pi - pi/12 - (7pi)/8 = pi/24`

Applying the Law of Sines,

`a / sin (pi/12) = 12 / sin(pi/24) = c / sin ((7pi)/8)`

`a = (12 * sin (pi/12)) / sin (pi/24) = 23.79`

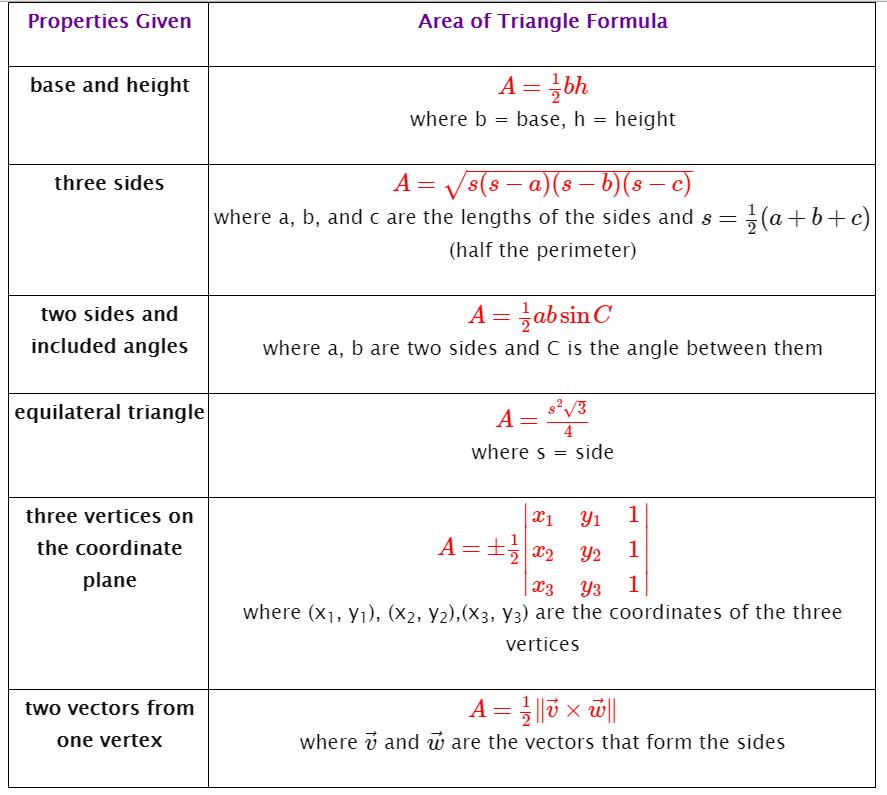
Knowing two sides a,b and the included angle C, to find the area we can use the formula `color(crimson)(A_t = (1/2) a b sin C`

`A_t = (1/2) * 23.79 * 12 * sin((7pi)/8) = color(purple)(54.62 " sq units"`